1.1. Sekantensteigung
Eine Sekante ist eine Gerade, die durch 2 Punkte einer Kurve geht (lat. secare = schneiden).
Schauen wir uns den Graphen von f(x) = x² an.
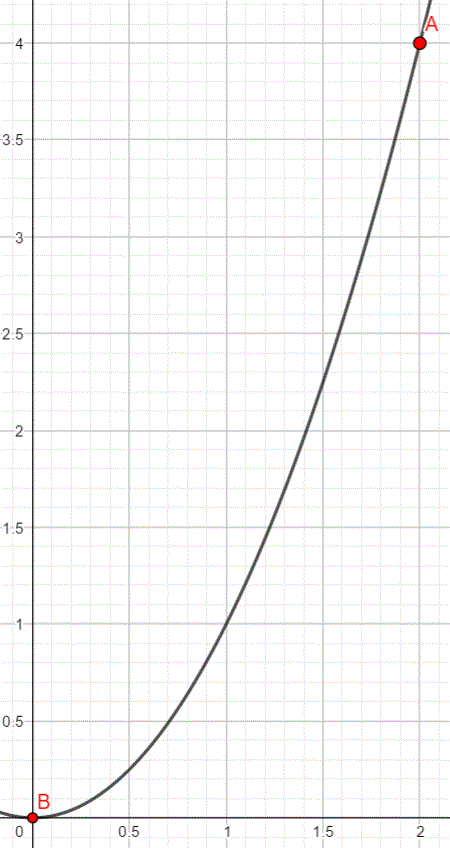
Nun wählen wir 2 Punkte auf der Parabel aus, A(2/4) und B(0/0).
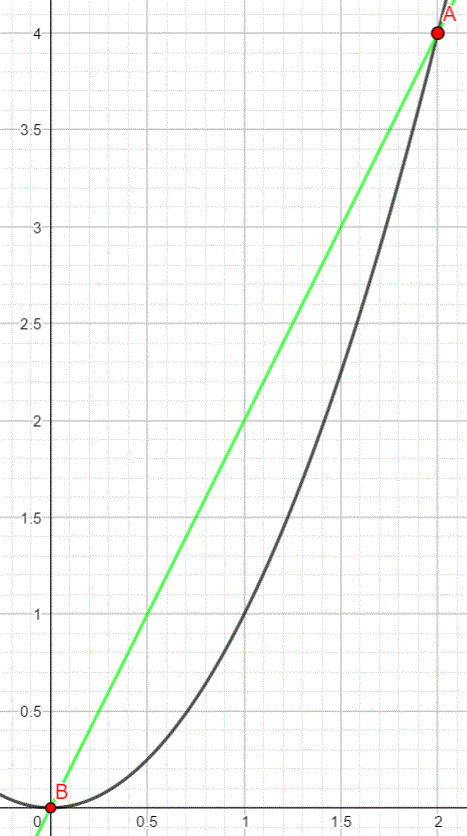
Durch die Punkte A und B zeichnen wir nun die Sekante.
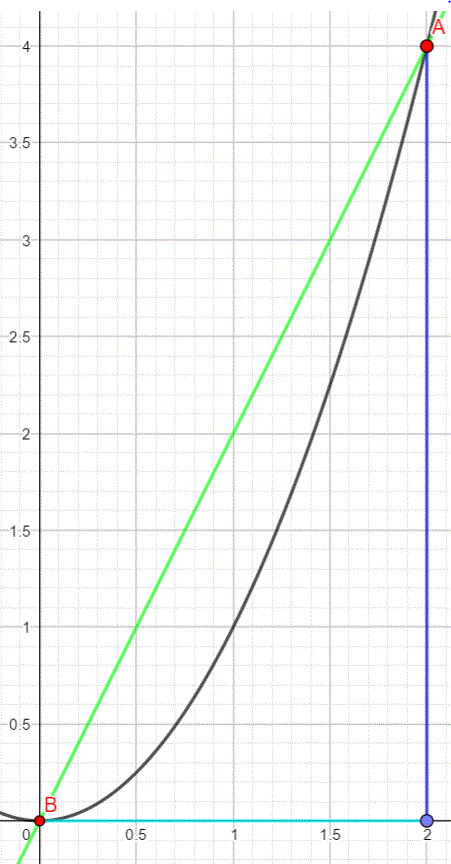
Die Steigung der Sekante berechnen wir mittels des Steigungsdreiecks. Die Formel zur Berechnung der Steigung ist aus Klasse 9 bekannt und lautet: m = \frac{f(x_{1}) - f(x_{0})}{x_{1} - x_{0}} . Diese Formel nennt man Differenzenquotient.
Aus A(2/4) und B(0/0) lesen wir heraus: x _{0} = 0 und x_{1} = 2 .
Diese Werte setzen wir in die Gleichung für die Sekantensteigung ein und erhalten: m = \frac{f(2) - f(0)}{2 - 0} = \frac{4 - 0}{2} = 2
Die Sekante hat somit die Steigung m = 2.
Mit dem Differenzenquotienten kann man die Steigung im entsprechenden Intervall berechnen. Mit ihm berechnet man also die Intervall- bzw. Sekantensteigung. Diese wird auch als mittlere Änderungsrate der Funktion im entsprechenden Intervall bezeichnet.
Übung