1.3. Quadratische Funktion
Funktionen des Typs f(x) = ax² + bx + c, mit …, nennt man quadratische Funktionen.
Da ihr höchster Exponent die 2 ist, werden sie auch Funktionen 2. Grades genannt.
Die Parameter a, b und c haben unterschiedliche Auswirkungen auf das Aussehen des Funktionsgraphen.
Wählt man a positiv, so ist die Parabel nach oben geöffnet.
Ist a negativ, so ist die Parabel nach unten geöffnet.
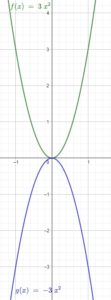
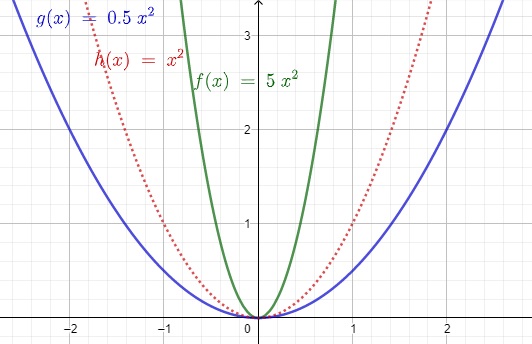
Ist a größer als 1, so ist die Parabel enger als die Normalparabel (f(x) = 1x²).
Ist a kleiner als 1, so ist die Parabel breiter als die Normalparabel.
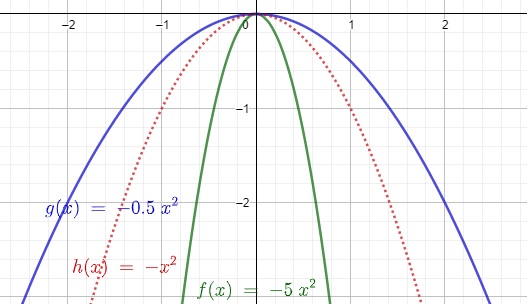
Wie sieht die Parabel aus, wenn a negativ und ungleich 1 ist?
Man sieht, dass die obigen Beziehungen ebenfalls gelten, allerdings ist die Parabel jeweils nach unten geöffnet.
Die Weite der Öffnung hängt also vom Betrag von a ab.
Es gilt somit:
|a| > 1: Die Parabel ist enger als die Normalparabel
0 <|a| < 1 : die Parabel ist breiter als die Normalparabel.
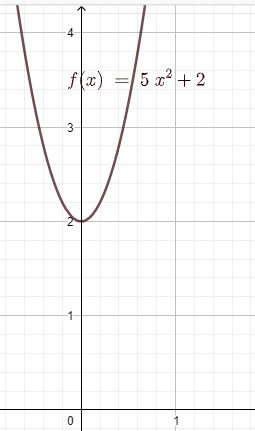
Der Parameter c (f(x) = ax² + bx + c) gibt die Verschiebung der Parabel bzgl. der y-Achse an.
Zu den Funktionswerten von f(x) = ax² wird jeweils der Summand c hinzuaddiert, was zur Folge hat, dass die Funktion f(x) = ax² um den Summanden c „hoch- oder runterrutscht“.
Lag der Scheitelpunkt von f(x) = ax² bei S(0/0), so liegt der Scheitelpunkt von f(x) = ax² + c nun bei S(0/c).
Funktionen der Form f(x) = ax² + bx + c muss man in die Scheitelpunktsform bringen, um den Scheitelpunkt ablesen zu können.
Diese lautet: f(x) = a(x – d)² + c. Aus ihr liest man den Scheitelpunkt S(d/c) ab.
Da der Scheitelpunkt in der 12. Klasse mittels Differentialrechnung recht einfach bestimmt werden kann, sei hier auf die Erklärung der quadratischen Ergänzung verzichtet.
Der Parameter b verschiebt die Parabel zusätzlich in horizontaler Richtung.
Animationen
Übungen
Zeichnen quadratischer Funktionen
Bestimmung der Funktionsgleichung, wenn der Scheitelpunkt und ein weiterer Punkt gegeben sind
Bestimmung der Funktionsgleichung aus drei gegebenen Punkten