1.2. Lineare Funktion
Funktionen des Typs f(x) = mx + b, mit ![]() nennt man lineare Funktionen.
nennt man lineare Funktionen.
Da ihr höchster Exponent die 1 ist, werden sie auch Funktionen 1. Grades genannt.
m beschreibt hier die Steigung und b den y-Achsenabschnitt.
Sind 2 Punkte gegeben, so kann man die Steigung mittels des Steigungsdreiecks ermitteln.
Wobei zu beachten ist, dass die zeichnerische Lösung oft ungenau sein kann. 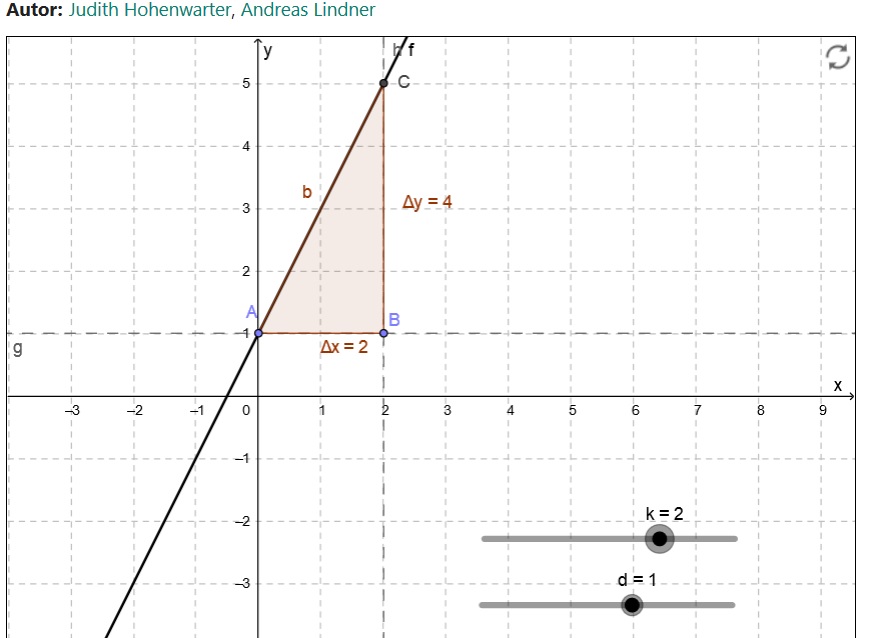
Daher gehen wir rechnerisch vor.
Sind zwei Punkte P1(x1/y1) und P2(x2/y2) gegeben, so gilt für die Steigung m: ![]()
Beispiel:
Sind die beiden Punkte A(3/6) und B(7/12) des Graphen einer linearen Funktion gegeben. Sie kann man daraus die zugehörige Funktionsvorschrift ermitteln.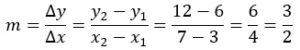
Für die Funktionsvorschrift der linearen Funktion gilt: f(x) = mx + b.
Mit x1 = 3 und y1 = 6 wissen wir nun: 6 = 1,5 * 3 + b.
Den Parameter b erhält man nun durch umstellen der Gleichung nach b. Es folgt b = 1,5.
Somit lautet die Funktionsvorschrift f(x) = 1,5 x + 1,5.
Möchte man die Schnittpunkte des Graphen mit den Achsen bestimmen geht man folgendermaßen vor.
Schnittpunkt mit der y-Achse: Für diesen Schnittpunkt gilt immer: x=0. Also folgt für f(x) = mx + b , f(0) = m*0 + b = b
Der Schnittpunkt mit der y-Achse hat also die Koordinaten Sy(0/b).
Schnittpunkt mit der x-Achse: Für diesen Schnittpunkt gilt immer: y=0. Man bestimmt also die Nullstellen.
Für y = 0 folgt also: f(x) = y = 0 = mx + b. Diesen Term stellt man nach x um und hat somit die Nullstelle bestimmt.
Für f(x) = 3x + 9 folgt: 3x + 9 = 0. Auflösen nach x liefert: x = –3. Sx(–3/0).
Um den Schnittpunkt zweier Graphen zu bestimmt setzt man diese gleich. Für f(x) = mx + b und g(x) = nx + c folgt dann f(x) = g(x).
Löse nun nach x auf, setze diesen Wert in eine der zwei Funktionen ein und bestimme auf diese Weise y.
f(x) = 2x+ 1; g(x) = x + 1. 2x + 1 = x + 1. x = 1 in f(x) oder g(x) einsetzen liefert: f(1) = 3. Also liegt der Schnittpunkt der zwei Geraden bei S(1/3)