5.7. Geradengleichung berechnen
Wie bestimt die Funktionsgleichung, wenn man zwei Punkte gegeben hat durch welche die Gerade verläuft?
Man bestimmt zunächst die Steigung und dann den y – Achsenabschnitt.
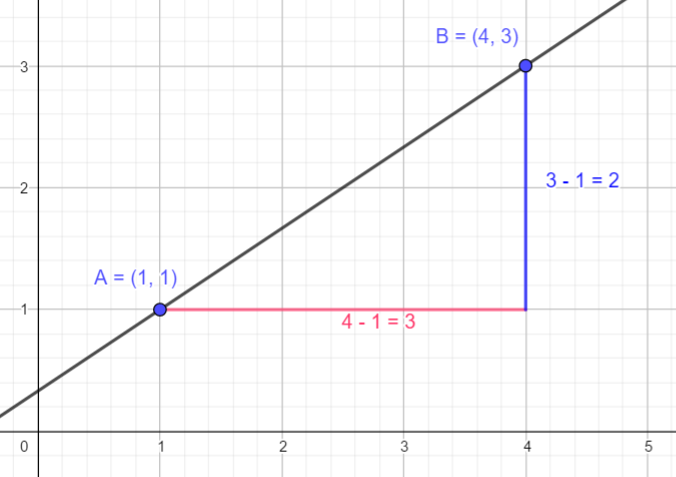
Gegeben sind die Punkte A(1/1) und B(4/3).
Durch das Steigungsdreieck kann man die Steigung bestimmen. Man sieht, dass man vom Punkt A(1/1) 3 Schritte nach rechts geht und von dort aus 2 Schritte nach oben, um beim Punkt B(4/3) anzukommen. Hieraus kann man die Steigung ermitteln.
m = \frac{3 - 1}{4 - 1} = \frac{2}{3}
Mit der Steigung kann man den y – Achsenabschnitt ermitteln. Man setzt hierzu m und den Punkt A oder B in die Geradengleichung y = mx + b ein.
Aus A(1/1) ergibt sich x = 1; y = 1. Das setzt man zusammen mit m = \frac{2}{3} in y = mx + b ein:
1 = \frac{2}{3} • 1 + b | – \frac{2}{3}
1 – \frac{2}{3} = b
\frac{3}{3} - \frac{2}{3} = \frac{1}{3} = b
Setzt man m und b in die Geradengleichung ein, dann erhält man die Funktionsgleichung, welche durch die Punkte A und B verläuft.
y = \frac{2}{3} x + \frac{1}{3}
Zur Probe setzt man einen der beiden Punkte in diese Funktionsgleichung ein:
3 = \frac{2}{3} • 4 + \frac{1}{3}
3 = \frac{8}{3} + \frac{1}{3}
3 = \frac{9}{3} = 3
Allgemein berechnet man die Steigung bei gegebenen Punkte folgendermaßen
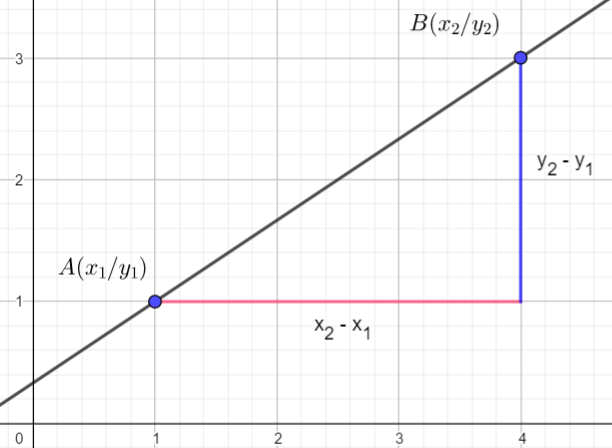
Mit den Koordinaten der beiden Punkte kann man die Abstände der beiden Punkte bestimmen.
m = \frac{y_{2} - y_{1}} {x_{2} - x_{1}}