1.4.1. Nullstellen der kubischen Funktion
Für die kubische Funktion gibt es keine (triviale) Lösungsformel.
Fehlt das absolute Glied bei einer kubischen Funktion, so lässt sich die erste Nullstelle durch ausklammern von x bestimmen –> x_{1} = 0. Die restlichen Nullstellen werden dann mittels der p-q-Formel berechnet.
Allgemein:
f(x) = ax³ + bx² + cx = 0 | x ausklammern
x(ax² + bx + c) 0 | x1 = 0
Wende auf ax² + bx + c die p-q-Formel an.
Beispiel: f(x) = 4x³ + 5x² – 6x
4x³ + 5x² – 6x = 0 | x ausklammern
x (4x² + 5x – 6) = 0 | x1 = 0
4x² + 5x – 6 = 0 | : 4
x² + 1,25x – 1,5 = 0 | p = 1,25; q = – 1,5
Mit x_{2/3} = -\frac{p}{2}\pm \sqrt{\frac{p^2}{4}-q} folgt: x_{2} = -2; x_{3} = 0,75
Ist die kubische Funktion in der Form f(x) = ax³ + bx² + cx + d gegeben, so muss man die erste Nullstelle raten. Die ausgedachte Zahl setzt man in die Fukion ein und prüft, ob des Ergebnis 0 lautet.
Nun dividiert man das Polynom ax³ + bx² + cx + d durch (x – x_{1} ). Aus dem berechneten Quotienten bestimmt man die restlichen Nullstellen mithilfe der p-q-Formel.
Beispiel: f(x) =x³ – 8x² + 20x – 16
Erste Nullstelle raten: f(2) = 0.
Daher folgt:
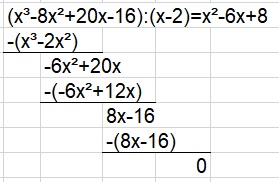
Die Polynomdivision liefert: (x³ – 8x² + 20x – 16) : (x – 2) = x² – 6x + 8
Wenn man auf x² – 6x + 8 die p-q-Formel oder abc – Formel anwendet erhält man als weitere Nullstellen x_{2} = 4 und x_{3} = 2.
Somit wäre x = 2 eine doppelte Nullstelle.
Übungen