4.3. Einheitskreis
Ein Kreis mit dem Radius 1 heißt Einheitskreis. Zu jedem Punkt P auf dem Einheitskreis gehört ein Winkel \angle A0P im Einheitskreis. Die Hypotenuse |0P| der Dreiecke 0AP und 0BP hat jeweils die Länge 1. Die Hypotenuse entspricht dem Radius im Einheitskreis welcher die Länge 1 hat.
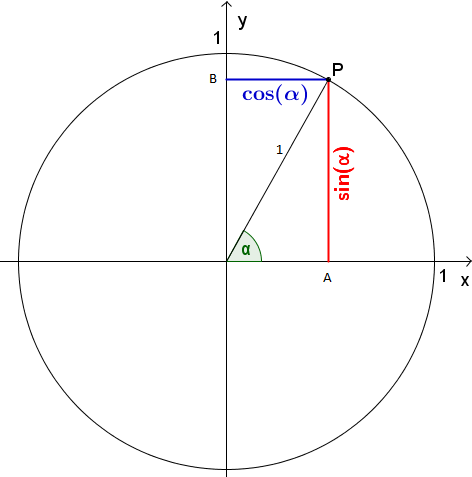
Es gilt \frac{|AP|}{|0P|} = sin \alpha . Da |0P| = 1, ergibt sich |AP| = sin \alpha .
Ebenso gilt \frac{|0A|}{|0P|} = cos \alpha . Da |0P| = 1, ergibt sich |0A| = cos \alpha .
Somit hat der Punkt P die Koordinaten (cos\alpha / sin\alpha)