1.2.5. Symmetrie
Es gibt zwei Arten von Symmetrie, die wir betrachten, die Punktsymmetrie und die Achsensymmetrie. Der Einfachheit halber betrachten wir aber nur die Punktsymmetrie zum Ursprung und die Achsensymmetrie zur y – Achse.
Achsensymmetrisch zur y- Achse ist eine Funktion genau dann, wenn der Graph auf der rechten Seite spiegelbildlich zum Graphen auf der linken Seite der y – Achse ist. Das ist genau dann der Fall, wenn f(-x) = f(x) ist. Das ist genau dann der Fall, wenn ausschließlich gerade Exponenten vorkommen.
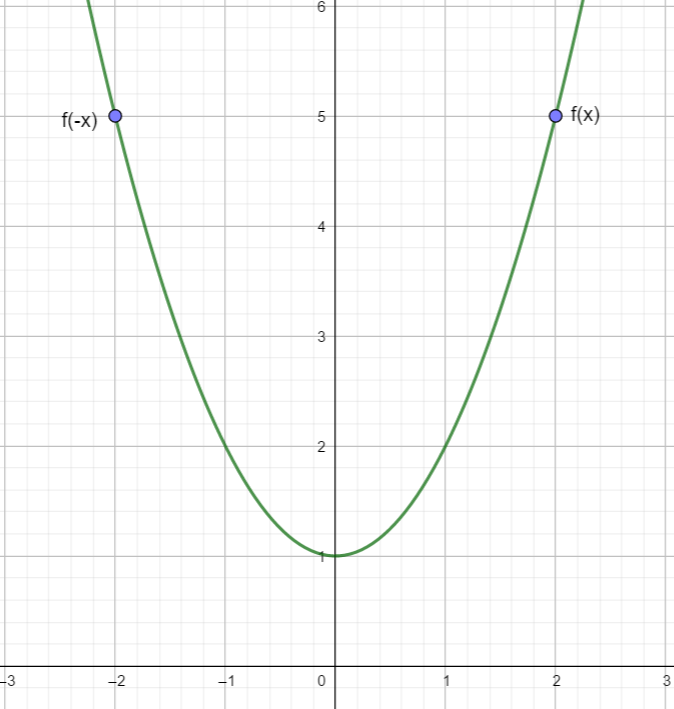
Im Beispiel ist f(x) = x² + 1.
Es ist f(2) = 4 und f(-2) = 4.
Allgemein ist im Beispiel f(-x) = (-x)² + 1 = x² + 1 = f(x).
Die Funktion f(x) = x² + 1 ist also achsensymmetrisch zur y – Achse.
Punktsymmetrisch zum Ursprung ist eine Funktion wenn f(-x) = -f(x) gilt. Dies ist genau dann der Fall, wenn ausschließlich ungerade Exponenten vorkommen und kein absolutes Glied vorhanden ist.
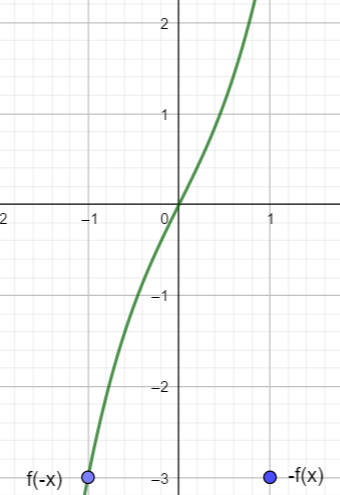
Im Beispiel ist f(x) = x³ + 2x.
Es ist f(-1) = -3 und -f(1) = -1 • 3 = -3
Allgemein ist im Beispiel f(-x) = (-x)³ + 2(-x) = -x³ – 2x
-f(x) = -1 • (x³ + 2x) = -x³ – 2x.
Die Funktion f(x) = x³ + 2x ist also punktsymmetrisch zum Ursprung.