1.6.1. Sonderfälle
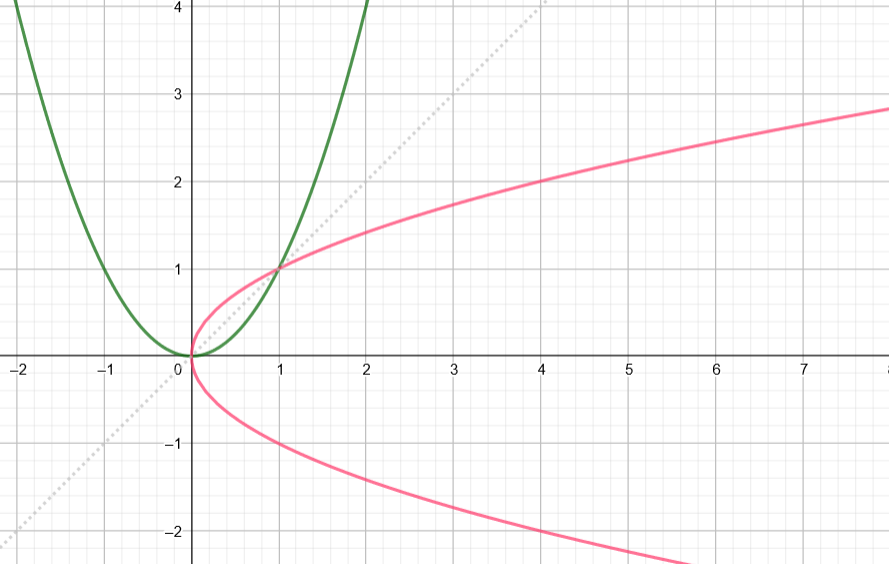
Wenn man den Graphen von f(x) = x² an der ersten Winkelhalbierenden spiegelt, dann erhält man folgenden Graphen.
Der rote Graph ist jedoch kein Graph einer Funktion, weil z. B. x = 2 zwei Funktionswerte zugeordnet werden würden. Es darf bekanntlich einem x – Wert nur ein y – Wert zugeordnet werden.
Graphisch kann man überprüfen, ob ein Graph einer Funktion vorliegt, indem man man überprüft, wie viele Schnittpunkte der vorliegende Graph mit einer parallelen zur y – Achse hat.
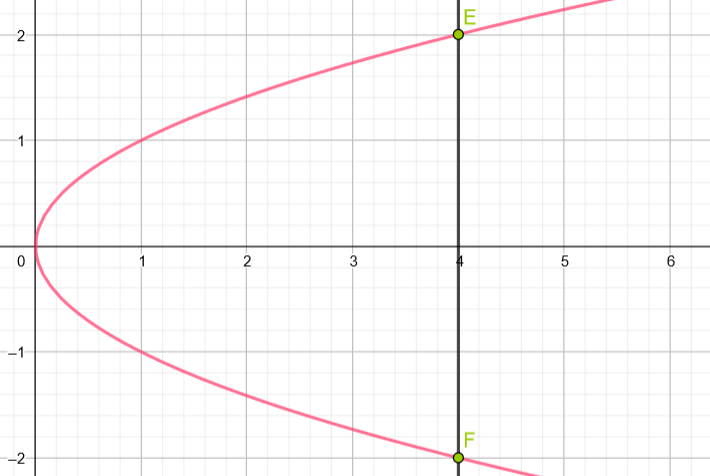
Man sieht, dass der vorliegende Graph zwei Schnittpunkte – E und F – mit einer zur y – Achse parallelen Geraden hat. Also kann dieser Graph nicht der Graph einer Funktion sein.
Man muss aber nicht erst den Graphen spiegeln, um zu sehen, ob man den Graphen einer Funktion erhält. Hat der Graph von f(x) mehr als einen Schnittpunkt mit einer zur x – Achse parallelen Geraden, so ist der gespiegelte Graph dazu kein Graph einer Funktion.
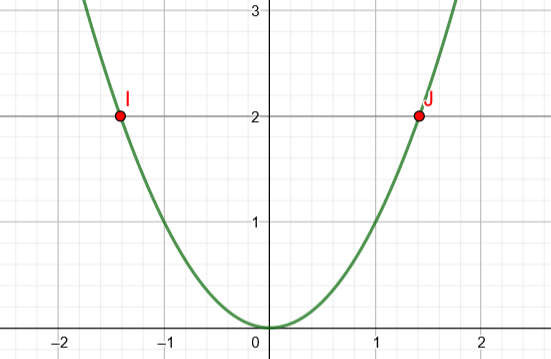
Man sieht, dass der Graph von f(x) = x² zwei Schnittpunkte einer zur x – Achse parallelen Geraden hat.
Folglich ist der, durch Speigelung an der ersten Winkelhalbierenden entstehende Graph, kein Graph einer (Umkehr-) funktion.
Wie sieht nun der Graph der Umkehrfunktion aus, bzw. wie bildet man diese rechnerisch?
y = x² | Wurzel ziehen
\pm \sqrt{y} = x | vertausche x und y
\pm \sqrt{x} = y
Der so entstehende Graph wäre, wie wir oben gesehen haben, kein Graph einer Funktion.
Die Lösung liegt darin, dass man den Definitionsbereich von f einschränkt. Damit der untere Ast verschwindet, dürfen in f nur positive Werte eingesetzt werden.
Für \mathbb{D} = \mathbb{R}^{+} ist f^{-1} = \sqrt{x}
Für \mathbb{D} = \mathbb{R}^{-} ist f^{-1} = -\sqrt{x}
Die Umkehrfunktion der quadratischen Funktion ist die Wurzelfunktion.