1.4.1. Exponentielles Wachstum
Das typische Beispiel für exponentielles Wachstum ist ein mit Algen bedeckter See.
Ein anfangs 500 m² großer See wird jede Woche durch Baggerarbeiten um 100 m² größer. Zu Beginn der Baggerarbeiten findet man einen Algenteppich mit 1 m² Größe, welcher pro Woche um das doppelte wächst. Wie verhält sich jeweils das Wachstum der See- und der Algenfläche?
| Woche | Fläche des Sees | Fläche der Algen |
| 0 | 500 m² | 1 m² |
| 1 | 600 m² | 2 m² |
| 2 | 700 m² | 4 m² |
| 3 | 800 m² | 8 m² |
| 4 | 900 m² | 16 m² |
| 5 | 1000 m² | 32 m² |
| 6 | 1100 m² | 64 m² |
| 7 | 1200 m² | 128 m² |
| 8 | 1300 m² | 256 m² |
| 9 | 1400 m² | 512 m² |
| 10 | 1500 m² | 1024 m² |
| 11 | 1600 m² | 2048 m² |
Man sieht, dass nach spätestens 11 Wochen der ganze See mit Algen bedeckt wäre.
Bei dem Wachstum der Wasserfläche liegt lineares Wachstum vor. Es kann durch die Funktion f(x) = 100x + 500, mit x = Anzahl der Wochen, beschrieben werden.
Bei dem Wachstum der Algenfläche liegt exponentielles Wachstum vor. es kann durch die Funktion f(x) = 2^{x} , mit x = Anzahl der Wochen, beschrieben werden.
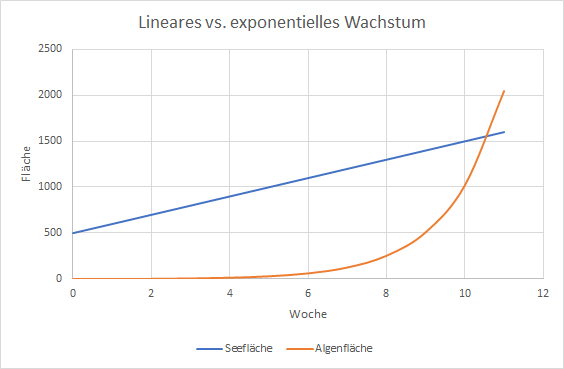
Man sieht, dass die Seefläche gleichmäßig ansteigt, hier liegt lineares Wachstum vor – der zugehörige Graph ist eine Gerade.
Die Fläche der Algen steigt anfangs sehr langsam und ab einem gewissen Zeitpunkt recht schnell. Jedesmal wenn x um 1 wächst, verdoppelt sich der Funktionswert. Hier liegt exponentielles Wachstum vor.
Lineares Wachstum: Zu gleichen Zeitspannen gehört immer eine Zunahme um den gleichen Betrag.
Exponentielles Wachstum: Zu gleichen Zeitspannen gehört immer eine Vervielfachung mit dem gleichen Faktor, dem Wachstumsfaktor.
Berechnung des Wachstumfaktors
Aus einer prozentualen Wachstumsrate kann man den Wachstumsfaktor berechnen.
Zu einem Wachstum von +p% gehört der Wachstumfaktor q=1+\frac{p}{100}
Zu einer Abnahme von -p% gehört der Wachstumfaktor q=1-\frac{p}{100}
Als Faustregel für die Verdopplungszahl kann man die Formel p • n \approx 70 , mit n = Anzahl der Perioden, verwenden. Diese Faustregel gilt allerdings nur bei kleinen Prozentsätzen bis ca. 12%.
Eine Bakterienkultur wächst pro Woche um 8 %.
Berechne zunächst den Wachstumsfaktor q. q=1+\frac{8}{100} = 1,08
Die zugehörige Funktionsvorschrift lautet f(x) = 1,08^{x}
Ein radioaktives Element hat eine Halbwertszeit von 25 Tagen.
Berechne zunächst den Wachstumsfaktor q. q=1-\frac{50}{100} = 0,5
Die zugehörige Funktionsvorschrift lautet f(x) = 0,5^{x} , wobei x ein Vielfaches von 25 Tagen entspricht.
Übung
Lineares / exponentielles Wachstum 1
Lineares / exponentielles Wachstum 2
Lineares / exponentielles Wachstum 3
Exponentielles Wachstum