1.4.3. Exponentialfunktionen
Die Funktion f(x) = 2^{x}, x \in \mathbb{R} heißt Exponentialfunktion zur Basis 2.
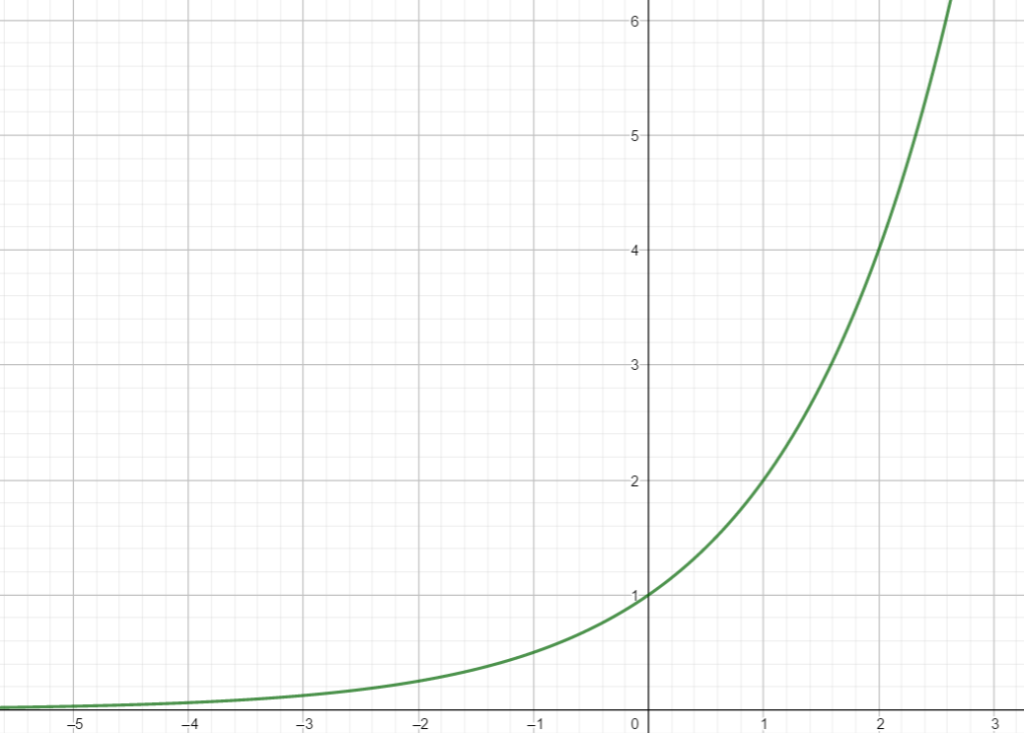
Für diese Funktion gilt:
- Sie ist monoton steigend.
- Der Graph liegt oberhalb der x – Achse.
Allgemein heißt die Funktion f(x) = b^{x}, x \in \mathbb{R}, b \in \mathbb{R} ^{+} \{1} Exponentialfunktion zur Basis b.
Exponentialfunktionen haben die Variable x im Exponenten.
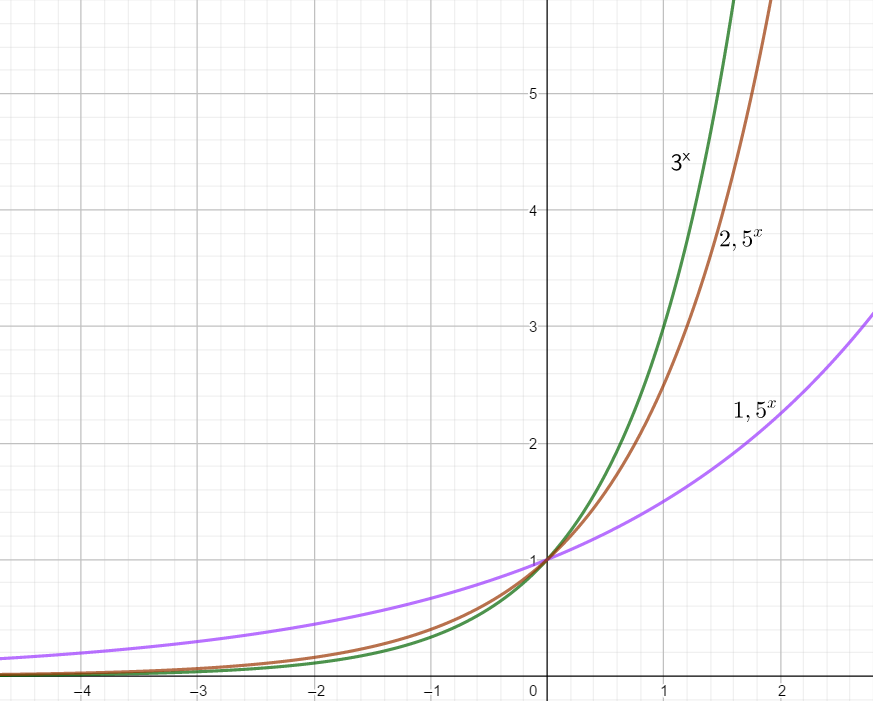
Man sieht, dass die drei Funktionen alle den gemeinsamen Punkt (0/1) haben, denn
f(0) = b^{0} = 1
Weiterhin sind sie alle monoton steigend und die Graphen liegen oberhalb der x – Achse.
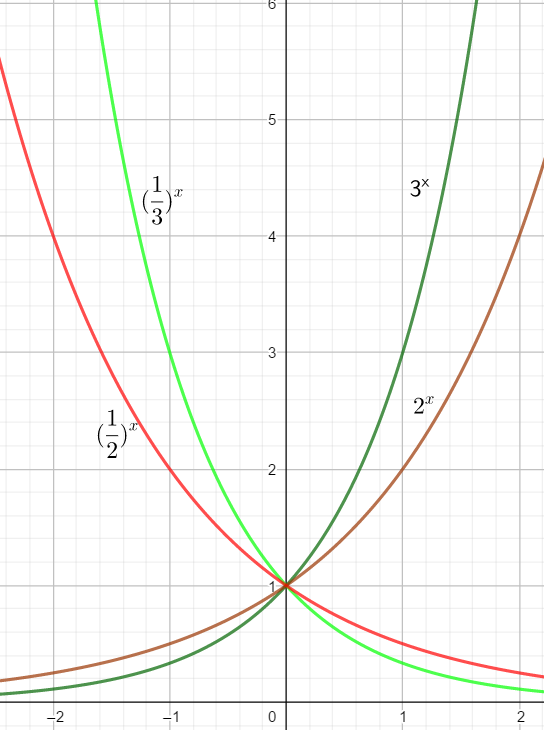
Die Graphen von f(x) = 3^{x}
und f(x) = (\frac{1}{3})^{x} sind symmetrisch zur y – Achse.
Allgemein sind die Graphen von f(x) = b^{x} und f(x) = (\frac{1}{b})^{x} symmetrisch zur y – Achse.
Sie haben jeweils den Punkt (0/1) gemeinsam.
Ebenso ist f(x) = f(-x), denn
f(-x) = (\frac{1}{b})^{-x} = (\frac{1}{\frac{1}{b}})^{x} = b^{x}
Eigenschaften der Exponentialfunktionen
Für jede Exponentialfunktion f(x) = b^{x}, x \in \mathbb{R} gilt:
Der Graph der Funktion
– steigt für b > 1
– fällt für 0 < b < 1.
Der Graph liegt oberhalb der x – Achse.
Der Graph nähert sich asymptotisch dem
– negativen Teil der x – Achse für b > 1
– positiven Teil der x – Achse für 0 < b < 1.
Jedesmal, wenn x um 1 wächst, wird der Funktionswert f(x) = b^{x} mit dem Faktor b multipliziert.
f(x) = a•b^{x}
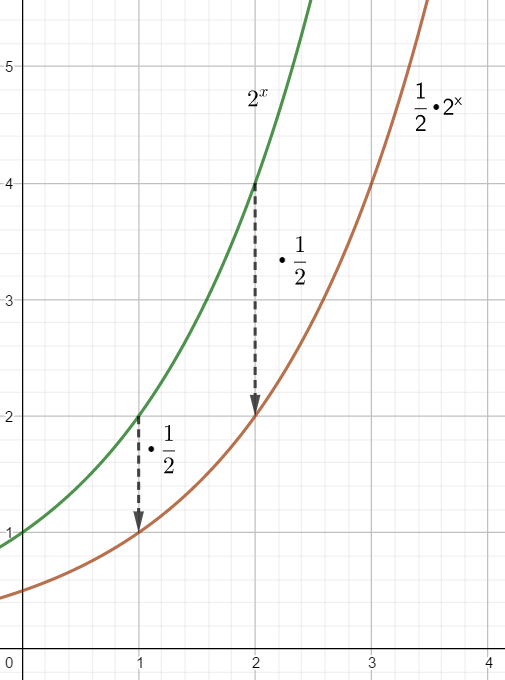
Man sieht, dass jeder Funktionswert der Funktion von f(x) = 2^{x} mit dem Faktor 0,5 multipliziert wird und man dadurch f(x) = \frac{1}{2}•2^{x} erhält.
Die Funktion f(x) = a•b^{x} , x \in \mathbb{R}, a \in \mathbb{R} ^{+}, b \in \mathbb{R} ^{+}\{1} wird auch als Exponentialfunktion bezeichnet.
Man erhält den Graphen von f(x) = a•b^{x} aus dem von f(x) = b^{x} durch Achsenstreckung mit dem Faktor a.
Exponentielles Wachstum bedeutet, dass das Wachstum durch die Exponentialfunktion f(x) = a•b^{x}, x \in \mathbb{R} beschrieben wird.
Liegt ein exponentieller Wachstumsprozess im eigentlichen Sinne vor, dann ist die Basis b größer als 1. Bei einem exponentiellen Abnahmeprozess liegt die Basis b zwischen 0 und 1.
Wenn man weiß, dass der Graph einer Exponentialfunktion durch einen Punkt geht, dann kann man die zugehörige Exponentialfunktion rechnerisch bestimmen.
In diesem Beispiel soll der Graph der Exponentialfunktion f(x) = b^{x} durch den Punkt P(4/16) verlaufen. Aus P(4/16) liest man x = 4 und y = 16 heraus. Dies setzt man in die Funktionsvorschrift ein und erhält: 16 = b^{4} und löst dann schrittweise nach b auf.
16 = b^{4} | \sqrt[4]{}
x = \sqrt[4]{16} = 2
Die gesuchte Exponentialfunktion lautet also f(x) = 2^{x}
Ähnlich kann man auch die Funktionsvorschrift bzgl. f(x) = a•b^{x} bestimmen.
Im Beispiel soll der Graph der Exponentialfunktion f(x) = a•b^{x} durch die Punkte A(2/1) und B(3/5) verlaufen. Man setzt jeweils die Werte von x und y in die Funktionsvorschrift ein und erhält somit 2 Gleichungen.
1 = a•b^{2} und 5 = a•b^{3} | Löse die erste Gleichung nach a auf, um sie in die zweite einzusetzen.
a = \frac{1}{b^{2}} | Setze a in die zweite Gleichung ein
5 = \frac{1}{b^{2}}•b^{3} = b | Setze nun b = 5 in a = \frac{1}{b^{2}} ein
a = \frac{1}{5^{2}} = \frac{1}{25}
Die gesuchte Funktionsvorschrift lautet somit f(x) = \frac{1}{25} • 5^{x}
Um Textaufgaben zu lösen, muss man wissen, dass a der „Startwert“ und b der „Wachstumsfaktor“ ist.
Es zerfällt z. B. ein radioaktives Element, so dass die anfängliche Masse von 30 g jährlich um 10 % abnimmt. Da man von 30 g ausgeht ist a = 30 g. Aus der Abnahme von 10 % ermittelt man den Wachstumfsfaktor b = 0,9. Die entsprechende Funktionsvorschrift lautet somit f(x) = 30•0,9^{x} , x entspricht der Zeit.
Übung
Exponentialfunktion 1
Exponentialfunktion 2
Exponentialfunktion 3