3.6. Abstände
Abstand in der Ebene
Den Abstand zweier Punkte A in der Ebene bestimmt man mithilfe des Satzes von Pythagoras.
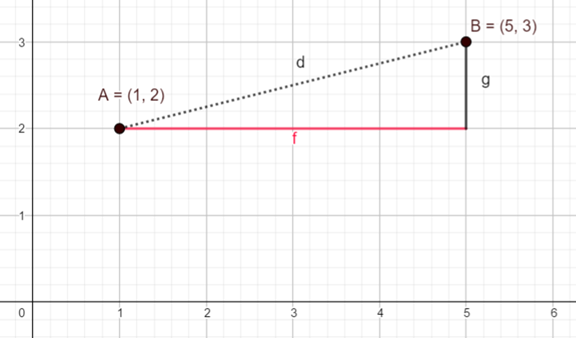
Um nun zu schauen wie weit der Punkt A(1/2) von Punkt B(5/3) entfernt ist benötigt man zunächst die Längen der Katheten. Diese ermittelt man, indem man jeweils die Abstände der Punkte auf der x- bzw. der y-Achse ermittelt.
Abstand auf der x-Achse: |x1 – x2| = |1 – 5| = 4 LE
Abstand auf der y-Achse: |y1 – y2| = |2 –3| = 1 LE
Nun wendet man hierauf den Satz des Pythagoras an und erhält den Abstand der zwei Punkte.
d² = 4² + 1² = 17 | \sqrt{}
d = \sqrt{17} LE
Die allgemeine Formel lautet somit: d = \sqrt{(x_2 - x_1)² + (y_2 - y_1)²}
Abstand von Punkt und Gerade
Möchte man den Abstand eines Punktes von einer Geraden bestimmen, so überlegt man sich zunächst was man mit den vorhandenen Mitteln berechnen kann.
Wir können den Abstand zwischen zwei Punkten bestimmen. Doch haben wir nur einen Punkt, den gegebenen.
Wir wissen, dass die kürzeste Verbindung über die Senkrechte geht. Diese können zu einer gegebenen Geraden bestimmen. Zusätzlich soll diese Senkrechte durch den gegebenen Punkt verlaufen.
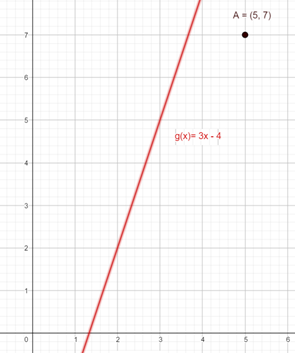
Gegeben sei nun ein Punkt A(5,7) und eine Gerade g mit g(x) = 3x – 4.
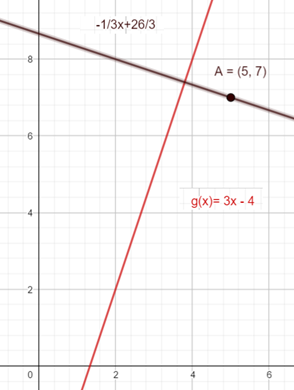
Wir bestimmen als erstes die zu g orthogonale Gerade f. Für die Steigung gilt: m_f = -\frac{1}{m_g} = -\frac{1}{3} . Da die Gerade natürlich durch den Punkt A gehen soll, müssen wir die Koordinaten von A in die Geradengleichung f(x) = mx + b bzw. y = mx + b einsetzen. Es folgt: 7 = -\frac{1}{3} • 5 + b. Umstellen nach b ergibt b = \frac{26}{3} . Somit ergibt sich
f(x) = -\frac{1}{3}x + \frac{26}{3}
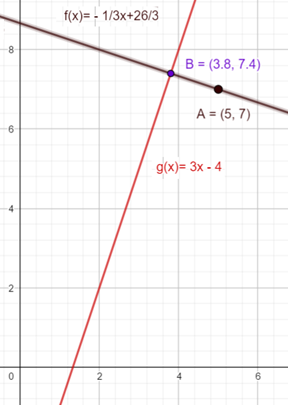
Wir brauchen aber immer noch unseren zweiten Punkt, da wir den Abstand zwischen 2 Punkten ja bestimmen können. Dieser zweite Punkt liegt auf der Geraden f. Und zwar genau dort, wo die Gerade g die Gerade f schneidet. Den Schnittpunkt zweier Geraden bestimmen wir durch Gleichsetzen der beiden Gleichungen: f(x) = g(x).
-\frac{1}{3}x + \frac{26}{3} = 3x - 4 | - \frac{26}{3}
-\frac{1}{3}x = 3x – 4 – \frac{26}{3} | – 3x
-\frac{1}{3}x - 3x = – \frac{12}{3} – \frac{26}{3} | : – 3\frac{1}{3}
x = 3,8
Setze x = 3,8 in f(x) oder g(x) ein.
g(3,8) = 3 • 3,8 – 4 = 7,4
Nun setzt man die Koordinaten von A und B in
d = \sqrt{(x_2 - x_1)² + (y_2 - y_1)²} ein und erhält
d = \sqrt{(5 - 3,8)² + (7 - 7,4)²} = 1,26 LE