1.2.4. Asymptote
Unter der Asymptoten versteht man eine Gerade oder eine Parabel, der sich der Funktionsgraph immer mehr annähert, je weiter man auf der x-Achse in Richtung +∞ oder −∞ geht.
Wie kann man die Funktionsgleichung der Asymptoten bestimmen? Man dividiert mittels Polynomdivision den Zähler durch den Nenner. Das Divisionsergebnis stellt dann die Asymptotengleichung dar. Dabei bleibt natürlich ein Rest übrig. Dieser wird für x → +∞oder x →−∞ dann sehr klein, er geht gegen Null.
Anschaulich kann man sagen, dass der Abstand zwischen dem Funktionsgraphen und der Asymptoten sehr klein wird, wenn man auf der x-Achse nur weit genug nach links oder rechts geht.
Nehmen wir die Funktion f(x) = \frac{x³ - 3x² - 4x}{x² - 6x + 8} .
Wenn man den Zähler durch den Nenner dividiert ergibt sich:
\: \: \: \: (x³ - 3x² - 4x) : (x² - 6x + 8) = x + 3
\underline {-(x³ - 6x² + 8x)}
\hspace*{0.9cm} (3x² - 12x)
\hspace*{0.6cm} \underline {-(3x² - 12x + 24)}
\hspace*{2.1cm} 6x - 24
Man erhält also f(x) = \frac{x³ - 3x² - 4x}{x² - 6x + 8} = x + 3 + \frac{6x - 24}{x² - 6x + 8}.
Strebt x nun gegen +∞ oder −∞, so strebt auch der Rest gegen 0. Es bleibt x + 3 übrig. Die Asymptote hat also die Gleichung a(x) = x + 3.
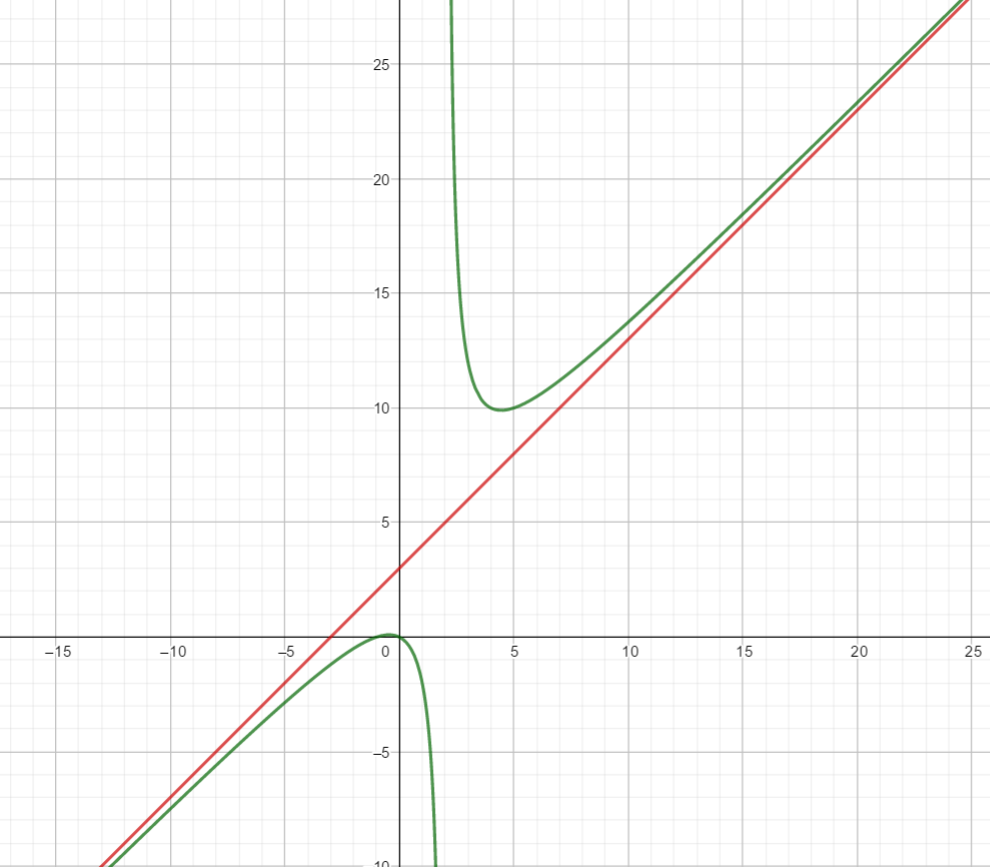
Der Graph von f (grün) nähert sich dem Graphen der Asymptoten (rot) immer weiter an, je weiter man auf der x-Achse in Richtung +∞ oder −∞ geht.
(Quelle: https://dk4ek.de/lib/exe/fetch.php/gebrfkt.pdf)