3.3. Exponentielles Wachstum
Wenn eine Größe in gleich großen Abschnitten um den gleichen Prozentsatz wächst, liegt exponentielles Wachstum vor. Die Größe verändert sich dabei von mal zu mal immer um den gleichen Faktor.
200 € werden zu einem Prozentsatz von 4,6 % angelegt.
Der Wachstumsfaktor q ist dann 1,046
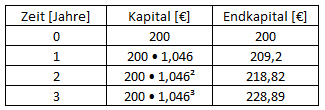
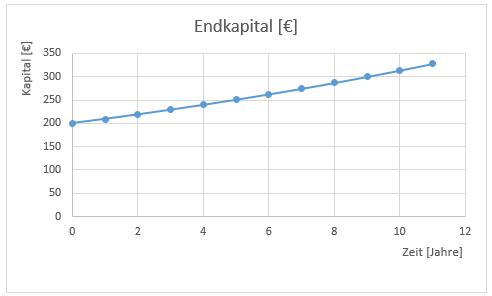
Man sieht, dass der Graph keine Gerade ist.
Allein an den wenigen Werten aus der obigen Tabelle kann man sehen, dass in gleichen Abständen immer mehr Geld hinzukommt.
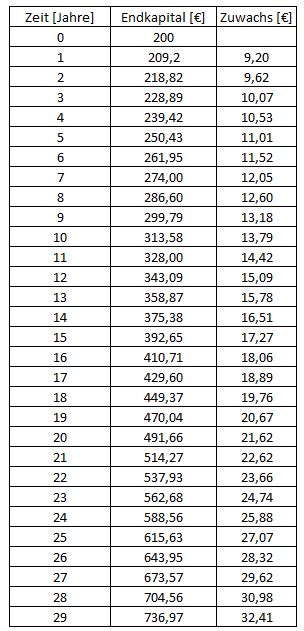
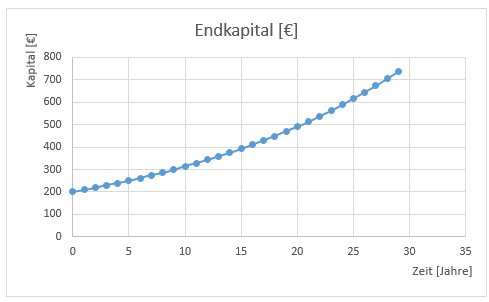
Der Graph beim
exponentiellen Wachstum
steigt anfangs relativ
langsam und wird dann
immer steiler.
Die Forme, mit der man exponentielles Wachstum berechnet lautet: G _{n} = G_{0} • (1 + \frac{p}{100})^n
Da (1 + \frac{p}{100})^n = q kann man obige Formel auch in der Art G_{n} = G_{0} • q^n schreiben.
Ersetzt man G durch K, so erhält man die sogenannte Zinseszinsformel K _{n} = K_{0} • (1 + \frac{p}{100})^n.
Nehmen wir unser Beispiel vom Anfang. Das Anfangskapital wäre dann K_{0} = 200 € . Aus dem Prozentsatz 4,6 berechnet sich q = 1,04. Die Formel, mit der man das Kapital im n – ten Jahr berechnet lautet dann
K _{n} = K_{0} • (1 + \frac{p}{100})^n
K _{n} = 200 • (1 + \frac{4,6}{100})^n
K_{n} = 200 • 1,046^n.
Somit hätte man z. B. nach dem 10. Jahr K_{10} = 200 • 1,046^{10} = 313,58 €
Übung