5.2. Graph der linearen Funktion
Der Graph der linearen Funktion ist eine \textbf{Gerade} .
Schauen wir uns als Beispiel die Funktion f(x) = 2•x + 1 an.
Um den Graphen dieser Funktion zu zeichnen, müssen wir zunächst eine \textbf{Wertetabelle} erstellen.
| x | 0 | 1 | 2 | 3 |
| y |
Als erstes setzen wir in f(x) = 2x + 1 für x den Wert \color{green} 0 ein. f( \color{green} 0 ) = 2• \color{green} 0 + 1 = 1.
Wir berechnen also den Funktionswert an der Stelle \color{green} 0 . Dieser lautet 1.
In die Wertetabelle tragen wir den, zur 0 gehörigen Funktionswert ein.
| x | 0 | 1 | 2 | 3 |
| y | 1 |
Genauso verfahren wir nun nacheinander mit den weiteren Werten, die für x in der Wertetabelle stehen.
f( \color{green} 1 ) = 2• \color{green} 1 + 1 = 3
f( \color{green} 2 ) = 2• \color{green} 2 + 1 = 5
f( \color{green} 3 ) = 2• \color{green} 3 + 1 = 7
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
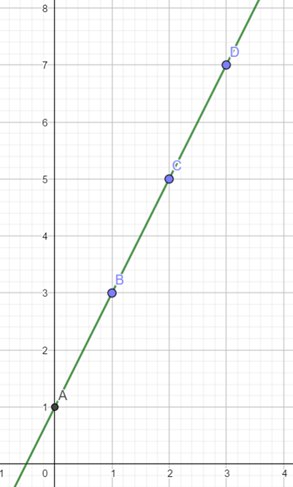
Die Paare (0/1), (1/3), (2/5) und (3/7) sind nun die Punkte, die wir ins Koordinatensystem eintragen und anschließend verbinden.
Man erkennt, dass der Graph eine Gerade ist. So wie im Beispiel geht man immer vor, wenn man zu einer Funktion den zugehörigen Graphen zeichnen soll. Man erstellt eine Wertetabelle, in welche man die berechneten Funktionswerte einträgt, und überträgt die Koordinaten in das Koordinatensystem. Dabei zeichnet man die Achsen so lang, dass der jeweils größte Wert für x und y auf den Achsen eingetragen werden kann
Wir zeichnen nun jeweils die Graphen der nachfolgenden Funktionen in ein Koordinatensystem.
f(x) = 2x + 2
f(x) = 2x + 3
f(x) = 2x + 5
| x | 0 | 1 | 2 |
| \color{red} y = 2x + 2 | 2 | 4 | 6 |
| \color{blue} y = 2x + 3 | 3 | 5 | 7 |
| \color{green} y = 2x + 5 | 5 | 7 | 9 |
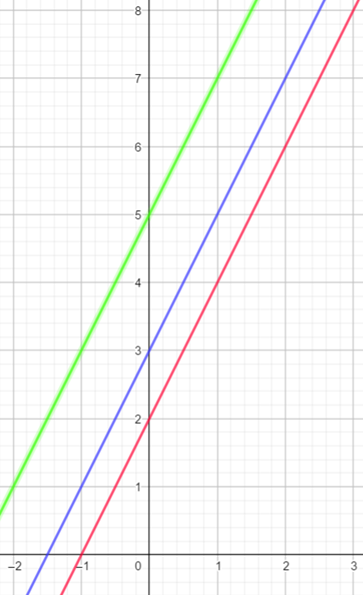
Man erkennt, dass die drei Graphen parallel verlaufen. Aber wovon hängt das ab?
Lineare Funktionen haben allgemein die Form f(x) = mx + b
bzw. y = mx + b.
Bei allen drei Funktionen ist dieses m, der Wert vor dem x, gleich. Das b unterscheidet sich. Bei genauem Hinsehen erkennt man, dass die jeweiligen Graphen die y-Achse jeweils bei den Werten des b schneiden, b wird daher auch \textbf{y-Achsenabschnitt} genannt.
Zeichnen wir nun die Funktionen
f(x) = 2x + 1
f(x) = 4x + 1
f(x) = 9x + 1
in ein gemeinsames Koordinatensystem.
| x | 0 | 1 | 2 |
| \color{green} y = 1x + 1 | 1 | 2 | 3 |
| \color{red} y = 4x + 1 | 1 | 5 | 9 |
| \color{blue} y = 9x + 1 | 1 | 10 | 19 |
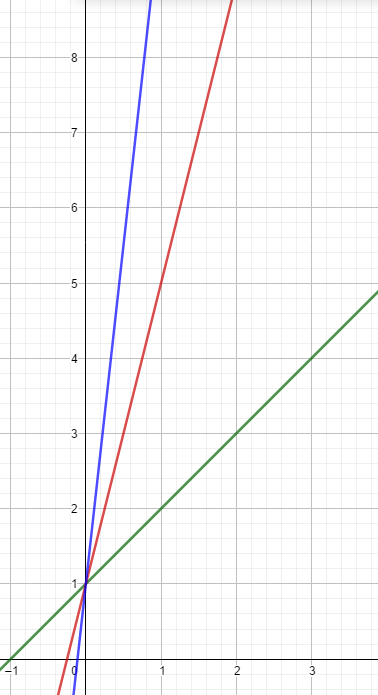
Man sieht, dass je größer die Zahl vor dem x, desto steiler die Gerade. Die Zahl vor x wird auch als Steigung bezeichnet.
Ist der Wert von m größer als 0, so ist die Steigung positiv.
f(x) = mx + b
Ist der Wert von m kleiner als 0, so ist die Steigung negativ.
f(x) = – mx + b
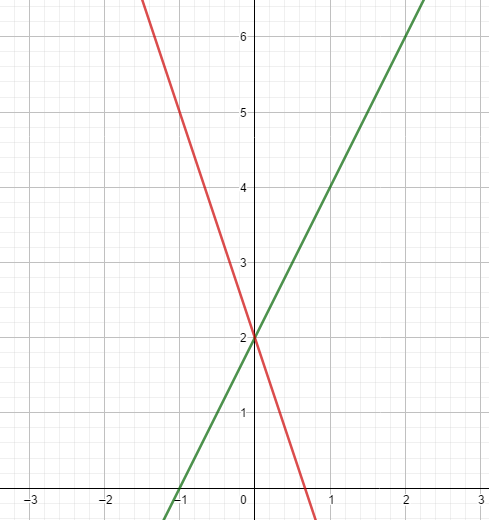
Schauen wir uns nun Beispiele mit positiver bzw. negativer Steigung an.
\color{green} f(x) = 2x + 2
\color{red} f(x) = -3x + 2
Übung