4.1. Rechtwinklige Dreiecke
In einem rechtwinkligen Dreieck gelten die folgenden Beziehungen.
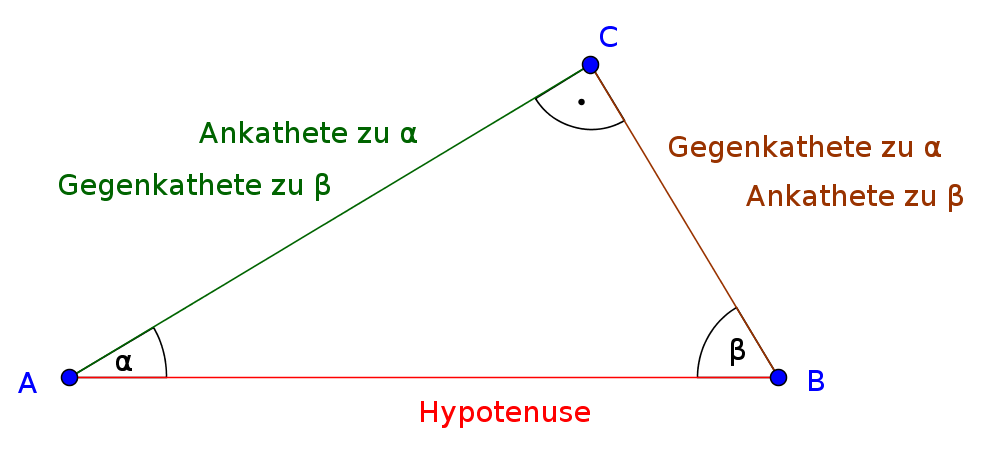
sin \alpha = \frac{Gegenkathete \ von \ \alpha}{Hypotenuse}
cos \alpha = \frac{Ankathete \ von \ \alpha}{Hypotenuse}
tann \alpha = \frac{Gegenkathete \ von \ \alpha}{Ankathete \ von \ \alpha}
Mithilfe dieser trigonometrischen Beziehungen lassen sich nun vielfältige Berechnungen am rechtwinkligen Dreieck durchführen.
Z. B. sei c = 8,4 cm; \alpha = 75° und \ \gamma = 90° . Dann sind die Seiten a und b, sowie der Winkel \beta gesucht.
sin \alpha = \frac{Gegenkathete \ von \ \alpha}{Hypotenuse} = sin \alpha = \frac{a}{c} | • c
a = c • sin \alpha = 8,4 • sin75° = 8,11 cm
Die Seite b könnte man nun mit dem Satz des Pythagoras oder mittels Trigonometrie ausrechnen.
cos \alpha = \frac{Ankathete \ von \ \alpha}{Hypotenuse} = cos \alpha = \frac{b}{c} | • c
b = c • sin \alpha = 8,4 • cos75° = 2,17 cm
\beta = 90° – 75° = 17°
Um das große Raätsel aufzulösen …
Kosinus“ ist in allen Kontexten richtig und entspricht auch der allgemeinen Richtlinie, nach der man das Präfix im Deutschen „Ko“ bzw. „ko“ schreibt. Im Duden-Universalwörterbuch verweist der Artikel „co-, Co-“ deshalb auch auf den Artikel „ko-, Ko-“:
ko-, Ko- [lat. co(n)- (< com-, cum) = mit-]: drückt in Bildungen mit Substantiven, Adjektiven und Verben ein partnerschaftliches Verhältnis, ein Mit- oder ein Nebeneinander aus:
Kodirektor, Koedition, koexistent, koexistieren
Quelle: https://www.matheretter.de/wiki/cosinus-kosinus-schreibweise#:~:text=%E2%80%9EKosinus%E2%80%9C%20ist%20in%20allen%20Kontexten,%2D%2C%20Ko%2D%20%5Blat.
Übung