8.6. Grenzwert von Folgen
Die Folge a _{n} = \frac{1}{n} hat die Folgeglieder 1; \frac{1}{2}; \frac{1}{3} . Diese kommen mit wachsendem n immer näher an die Null heran, ohne diese je zu erreichen.
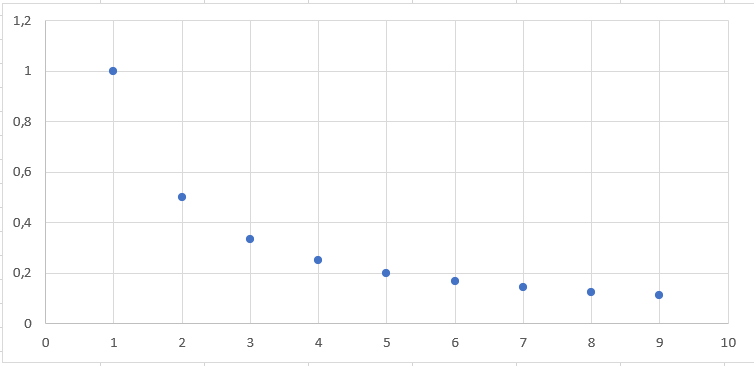
Man sieht, dass die Folgeglieder mit wachsendem n immer kleiner werden.
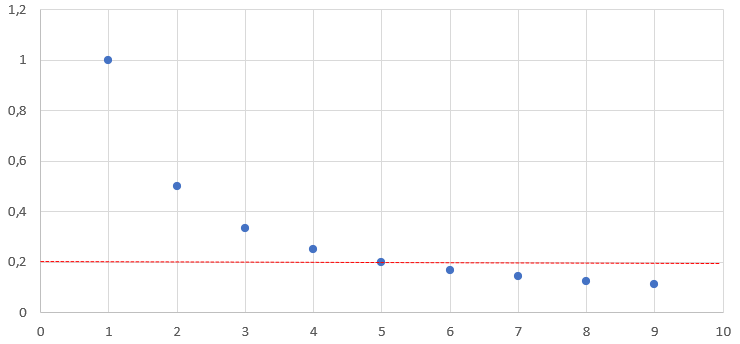
Man sieht, dass hier nur die ersten vier Folgeglieder außerhalb eines Streifens liegen, der die Breite 0,2 hat. Ab n > 5 liegen alle Folgeglieder innerhalb dieses Streifens.
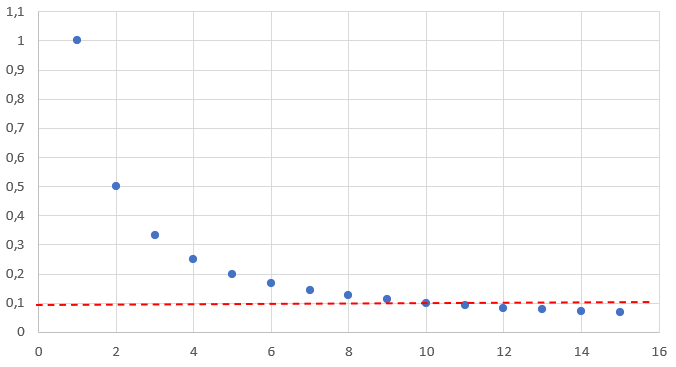
Man sieht, dass hier nur die ersten neun Folgeglieder außerhalb eines Streifens liegen, der die Breite 0,1 hat. Ab n > 10 liegen alle Folgeglieder innerhalb dieses Streifens.
Wir könnten die Breite des Streifens immer kleiner wählen und würden feststellen, dass eine endliche Menge an Folgegliedern außerhalb des Streifens und und enendlich viele innerhalb dieses Streifens.
Die Folge a _{n} = \frac{1}{n} hat den Grenzwert 0, weil es zu jeder noch so kleinen Zahl \epsilon > 0 eine Zahl S gibt, so dass \frac{1}{n} < \epsilon für alle n > S.
Zahlenfolgen mit dem Grenzwert 0 nennt man Nullfolgen.
Eine unendliche Zahlenfolge hat die Zahl g als Grenzwert, wenn zu jeder noch so beliebig kleinen positiven Zahl \epsilon eine natürliche Zahl S angegeben werden kann, für die gilt: n \geq S \Rightarrow |a _{n} - g | < \epsilon
Man schreibt \lim _{n \to \infty} a _{n} = g. („Limes a_{n} für n gegen unendlich gleich g“)
Folgen, die einen Geenzwert haben, werden konvergent genannt.
Eine Folge, die keinen Grenzwert hat, heißt divergent.
Diese Definition bedeutet, dass der Abstand zwischen den Folgegliedern und dem Grenzwert mit wachsendem n beliebig klein wird.
Beispiel:
Die Folge a _{n} = \frac{n}{n + 1} mit den Folgegliedern \frac{1}{2}; \frac{2}{3}; \frac{3}{4} ... hat vermutlich den Grenzwert g = 1.
Mit |a _{n} - g | < \epsilon folgt für unsere zu betachtende Folge | \frac{n}{n + 1} - 1 | < \epsilon \Rightarrow |\frac{n}{n+1} - \frac{n+1}{n+1} | < \epsilon Schreibt man als einen Bruch, so ergibt sich | \frac{n - (n + 1)}{n + 1} | < \epsilon \Rightarrow |\frac{1}{n+1} | < \epsilon , da alle Folgeglieder positiv sind, gilt \frac{1}{n + 1} < \epsilon
Multipliziere mit dem Nenner. 1 < \epsilon (n + 1) \Rightarrow \frac{1}{\epsilon} < n + 1 \Rightarrow \frac{1}{\epsilon} - 1 < n
Wie man auch immer \epsilon wählt, man findet immer ein S. In unserem Fall ist S = \frac{1}{\epsilon} - 1 so, dass für alle n > S gilt: | a _{n} - 1 | < \epsilon
Rechnen mit Grenzwerten
Der Grenzwert einer Summe (einer Differenz, eines Produkts) einzelner Folgen ist gleich der Summe (der Differenz, dem Produkt) der Grenzwerte der einzelnen Folgen.
Der Grenzwert eines Quotienten verschiedener Folgen ist gleich dem Quotienten der Grenzwerte, wenn der Grenzwert des Nenners von 0 verschieden ist.