8.3. Relative Häufigkeit
Wir wissen mittlerweile, dass die Wahrscheinlichkeit eine 6 zu würfeln genauso hoch ist wie für jede andere Zahl auch, nämlich \frac{1}{6} .
Bei einem Würfelspiel wie z.B. Mensch ärgere Dich nicht, kann es aber vorkommen, dass wir 6 mal würfeln und keine 6 dabei ist.
Würde man Würfeln und eine Strichliste bzgl. der 6 führen, dann würden sich z. B. folgende Werte ergeben.
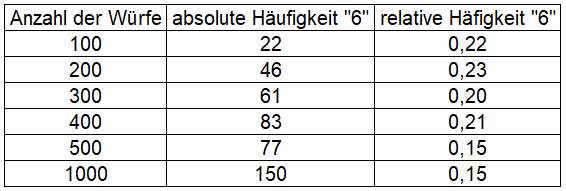
Die absolute Häufigkeit sagt aus wie oft die 6 bei der jeweiligen Anzahl der Würfe vorkam. Die relative Häufigkeit setzt diese Anzahl der 6en in Realtion zur Anzahl der Würfe.
Man sieht, dass sich die relative Häufigkeit der mathematischen Wahrscheinlichkeit angleicht. P(6) = \frac{1}{6} = 0,16 .
Dies ist als Gesetz der großen Zahlen bekannt. Je häufiger eine Zufallsexperiment durchgeführt wird, desto mehr nähern sich die relativen Häufigkeiten der mathematischen Wahrscheinlichkeit an.
Mit einem Würfelsimulator z. B. kann man viele Würfe simulieren.