1.5. Höhere Funktionen
Den Ausdruck a_{n}x^{n} + a_{n-1}x^{n-1} + a_{n-2}x^{n-2} + ... + a_{2}x^{2} + a_{1}x^{1} + a_{0} nennt man Polynom vom Grad n.
Den Grad liest man am höchsten vorkommenden Exponenten ab.
Die Zahlen vor den Variablen stehen werden Koeffizienten genannt.
Folglich nennt man f(x) = a_{n}x^{n} + a_{n-1}x^{n-1} + a_{n-2}x^{n-2} + ... + a_{2}x^{2} + a_{1}x^{1} + a_{0} Funktion vom Grad n.
Da es für Funktionen ab Grad 3 keine Lösungsformel gibt, müssen die Nullstellen mittels Polynomdivision oder Substitution bestimmt werden.

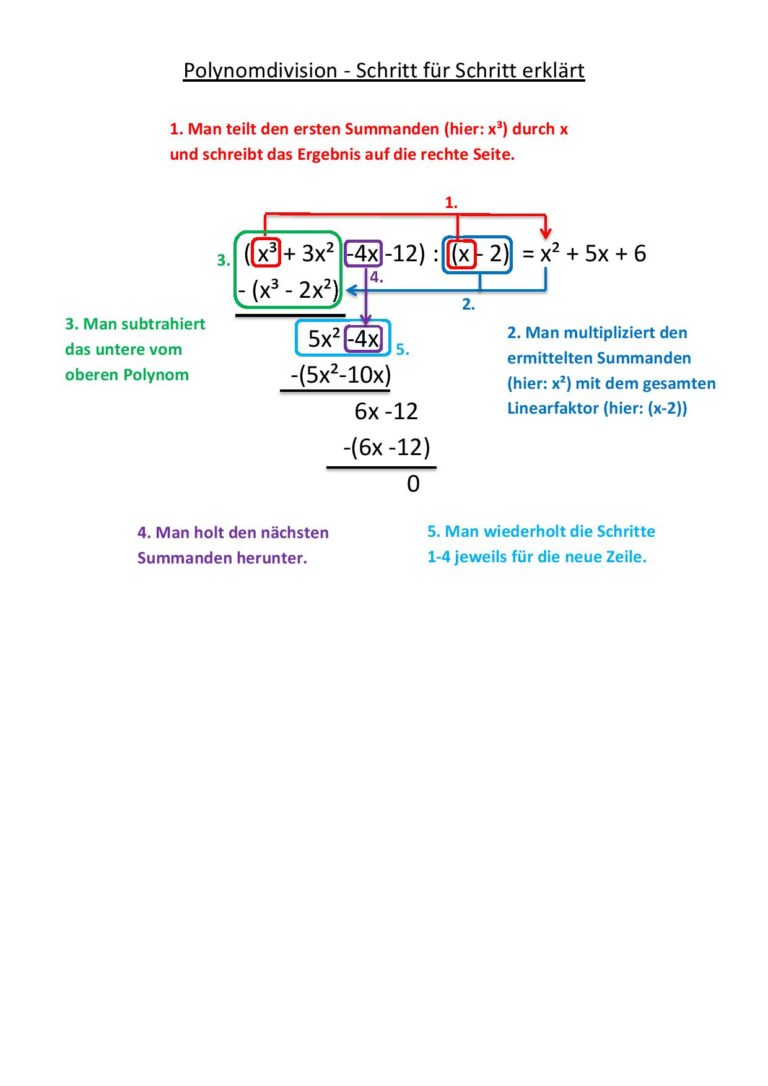
Übungen