3.3. Schnittpunkte mit den Achsen
Der Graph einer linearen Funktion schneidet die x – Achse und die y – Achse jeweils einmal. In der Mathematik sind diese Schnittpunkte von großem Interesse.
Schnittpunkt mit der y – Achse
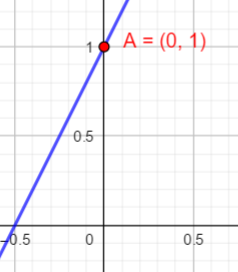
Der Schnittpunkt mit der y – Achse hat die Eigenschaft, dass die x – Koordinate immer 0 ist.
In diesem Beispiel lautet die Funktion y = 2x + 1. In diese Funktionsgleichung setzt man x = 0 ein und erhält: y = 2 • 0 + 1 = 1.
Der Punkt A(0/1) ist der Schnittpunkt mit der y – Achse.
Um den Schnittpunkt mit der y – Achse zu bestimmen, setzt man in die Funktionsgleichung für x immer 0 ein.
Schnittpunkt mit der x – Achse
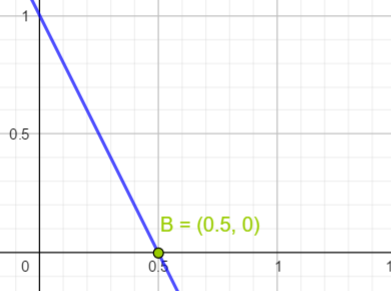
Der Schnittpunkt mit der x – Achse hat die Eigenschaft, dass y = 0 ist. Man geht also weder hoch noch runter, sondern bleibt auf der x – Achse.
In diesem Beispiel lautet die Funktion
y = -2x + 1. Man setzt für y = 0 ein und löst nach x auf:
0 = -2x + 1 | – 1
-1 = -2x | : (-2)
x = 0,5
Der Schnittpunkt mit der x – Achse hat also die Koordinaten (0,5/0).
Der Schnittpunkt mit der x – Achse wird auch Nullstelle genannt.
Um den Schnittpunkt mit der x – Achse zu bestimmen setzt man in die Funktionsgleichung für y immer 0 ein und löst nach x auf.
Übung