5.6. Parallele und senkrechte Geraden
Wann verlaufen zwei Geraden zueinander parallel?
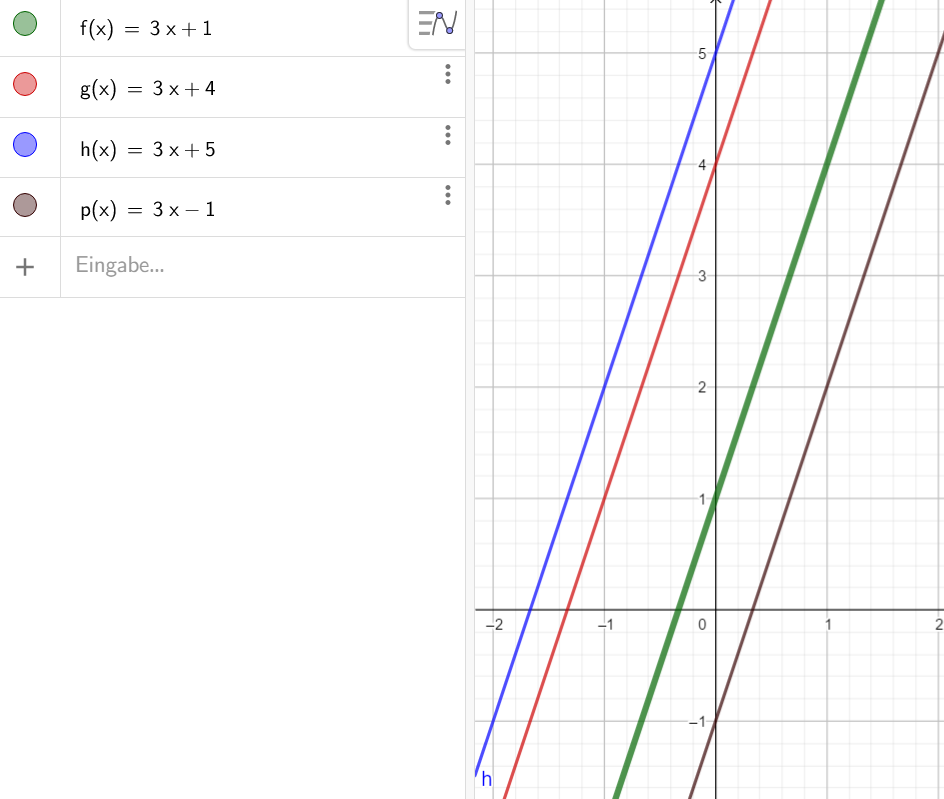
Die Graphen von g(x), h(x) und p(x) sind alle parallel zum Gaph von f(x).
Man sieht, dass alle vier Funktionen die gleiche Steigung haben. Der y – Achsenabschnitt ist unterschiedlich.
Geraden verlaufen parallel zueinander, wenn ihre Steigungen gleich sind.
Wann verlaufen Geraden senkrecht zueinander?
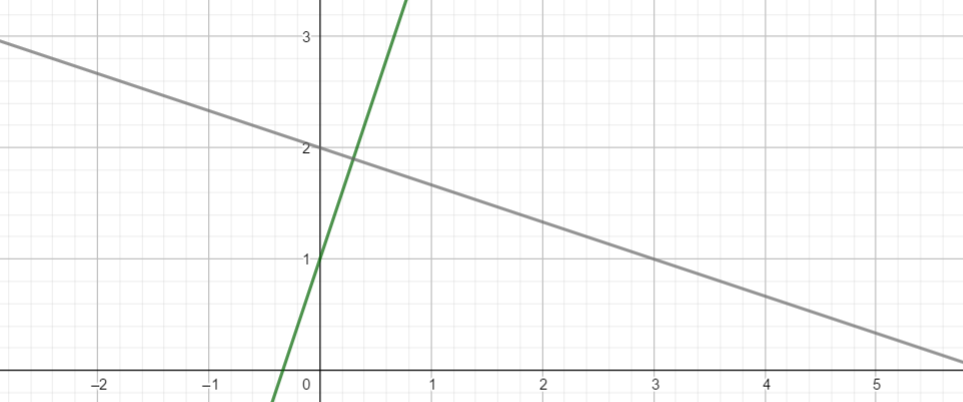
Die grüne Gerade ist der Graph von f(x) = 3x + 1, die schwarze Gerade ist der Graph von
g(x) = -\frac{1}{3}x + 2
Das Produkt der beiden Steigungen ist -1.
3 • ( -\frac{1}{3} ) = – 1.
Geraden sind dann senkrecht zueinander wenn für ihre Steigungen m_{1} und m_{2} gilt: m_{1} • m_{2} = -1
Ist die Steigung einer Funktion gegeben, dann kann man daraus die Steigung der dazu senkrechten Geraden berechnen.
Man formt hierzu m_{1} • m_{2} = -1 nach m_{2} um.
Der y – Achsenabschnitt kann beliebig gewählt werden.
m_{1} • m_{2} = -1 | : m_{1}
m_{2} = -\frac{1}{m_{1}}
Ist z. B. f(x) = 4x – 5, dann ist m_{1} = 4 und m_{2} = -\frac{1}{m_{1}} = -\frac{1}{4}
Ist z. B. f(x) = -5x + 7, dann ist m_{1} = -5 und m_{2} = -\frac{1}{m_{1}} = -\frac{1}{-5} = \frac{1}{5}
Ist z. B. f(x) = \frac{2}{3} x + 3, dann ist m_{1} = \frac{2}{3} und m_{2} = -\frac{1}{m_{1}} = -1 : m_{1} = -1 : \frac{2}{3} = -\frac{1}{1} • \frac{3}{2} = -\frac{3}{2}
Soll z. B. die zu f(x) = 3x + 2 senkrechte Gerade durch den Punkt A(3/5) verlaufen, so bestimmt man zunächst die
Steigung m_{2} .
m_{2} = -\frac{1}{m_{1}} = -\frac{1}{3}
Aus A(3/5) folgt, dass x = 3 und y = 5 ist. Man setzt beide Werte in y = m•x + b ein und erhält: 5 = -\frac{1}{3} •3 + b. Dies formt man nach b um.
5 = -\frac{1}{3} •3 + b = -\frac{3}{3} + b | + 1
6 = b
Die Probe ergibt: 5 = -\frac{1}{3} •3 + 6 = -1 + 6 Das ist eine wahre Aussage.
Die zu f(x) = 3x + 2 senkrechte Gerade lautet also g(x) = -\frac{1}{3} x + 6
Übungen
Parallele Geraden
Senkrechte Geraden 1
Senkrechte Geraden 2