1.4.4. Natürliche Exponentialfunktion
Die Folge (a_{n}) mit a_{n} = (1 + \frac{1}{n})^{n} ist konvergent. Ihr Grenzwert heißt eulersche Zahl und wird mit e bezeichnet. Die eulersche Zahl e ist eine irrationale Zahl und hat den Wert e = 2,71828…..
Die Funktion f(x) = e^{x}, x\in \mathbb{R} heißt natürliche Exponentialfunktion oder auch „e-Funktion“.
Die große Bedeutung der e – Funktion beruht auf der Tatsache, dass ihre Ableitung wieder die e – Funktion selbst ergibt.
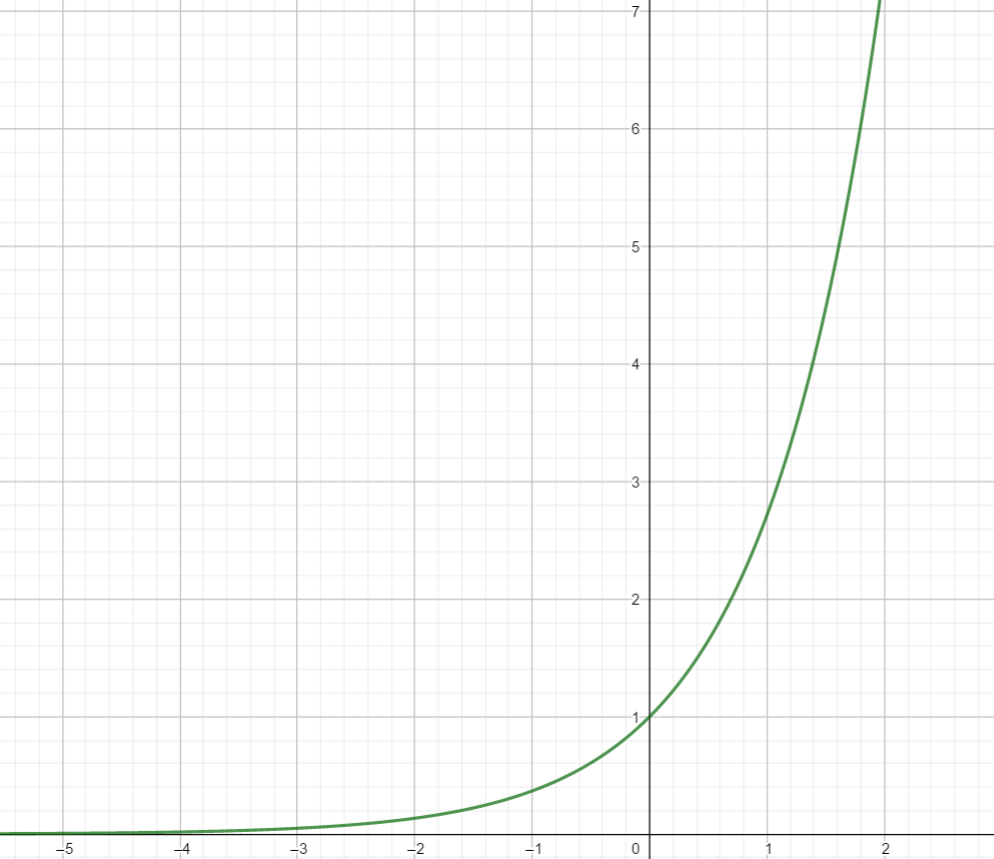
Der Graph der e-Funktion verläuft immer oberhalb der x – Achse. Der Graph nähert sich der x – Achse, schneidet sie aber nie. Das heißt, dass die e – Funktion keine Nullstellen besitzt.
Für \lim {x \to \infty} strebt e^{x} gegen unendlich.
Für \lim {x \to -\infty} strebt e^{x} gegen 0.
Der Graph der Exponentialfunktion heißt Exponentialkurve.