5.4. Steigungsdreieck
Man kann den Graphen einer linearen Funktion auch ohne Wertetabelle zeichnen.
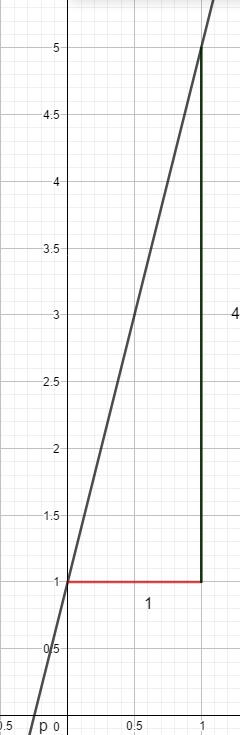
Aus z. B. f(x) = 4x + 1 kann man folgendes ablesen:
m = 4 (Steigung); b = 1 (y-Achsenabschnitt).
Wir setzen bei y = 1 einen Punkt, da der Graph bei (0/1) die y-Achse schneidet. Von diesem Punkt gehen wir 1 Einheit nach rechts und 4 Einheiten nach oben und setzen einen zweiten Punkt.
Um eine Gerade eindeutig zu zeichnen brauchen wir nur zwei Punkte. Durch diese zwei Punkte A(0/1) und B(1/5) können wir die Gerade nun zeichnen und erhalten den Grpahen der Funktion.
Allgemein gesehen markiert man zuerst den Punkt auf der y-Achse, das ist unser b. Dann geht man von diesem Punkt ausgehend so weit nach rechts wie es der Nenner angibt und so weit hoch wie es der Zähler angibt.
m = \frac{hoch}{rechts}
Ist die Steigung negativ, dann geht man statt nach oben nun nach unten.
– m = \frac{runter}{rechts}
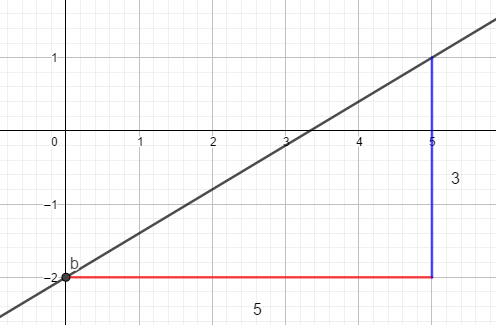
Für z. B. f(x) = \frac{3}{5}x - 2 ist m = \frac{3}{5} . Also geht man \frac{3 hoch }{5 rechts} beginnend vom Punkt (0/ – 2)
Das entstehende Dreieck nennt man Steigungsdreieck.