1.2. Lineare Gleichungssysteme
Ein lineares Gleichungssystem (LGS) besteht aus zwei linearen Gleichungen mit jeweils zwei Variablen. Da wo sich die beiden Geraden schneiden, liegen die Werte, für welche beide Gleichungen wahr sind. Sie sind die (gesuchte) Lösung des LGS.
Ein klassisches Beispiel für ein LGS ist folgende Aufgabe: In einem Stall leben Hasen und Hühner. Es sind insgesamt 9 Tiere, mit 24 Füßen. Wie viele Hasen und Hühner sind es jeweils?
Für die Anzahl der Anzahl der Hasen wählen wir die Variable x, für die der Hühner die Variable y.
Wir erhalten zwei lineare Gleichungen.
I: x + y = 9 –> Das ist die Gleichung für die Anzahl der Tiere
II: 4x + 2y = 24 –> Das ist die Gleichung für die Anzahl der Beine
Wir erstellen nun für beide Gleichungen den Graphen und zeichnen ihn in ein gemeinsames Koordinatensystem. Vorher ist allerdings darauf zu achten, dass wir jede Gleichung nach y auflösen müssen!
Aus I: x + y = 9 ergibt sich y = 9 – x
Aus II: 4x + 2y = 24 ergibt sich y = 12 – 2x
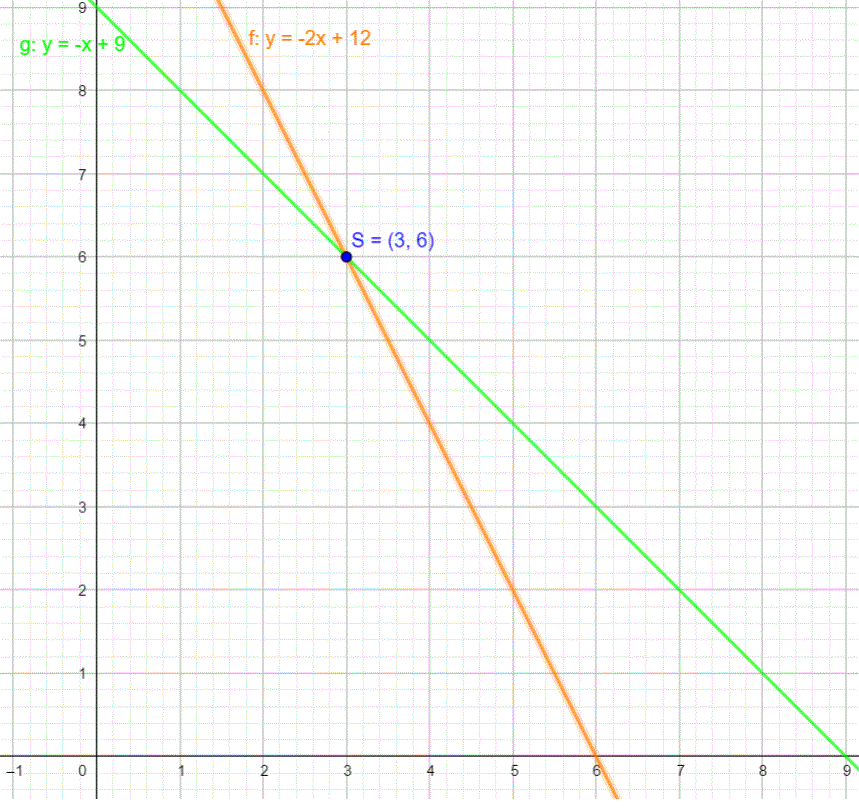
Beide Graphen schneiden sich im Punkt S(3 / 6). Aus S(3 / 6) lesen wir x = 3 und y = 6 ab. Da x für die Anzahl der Hasen und y für die Anzahl der Hühner steht, folgt, dass drei Hasen und sechs Hühner in dem Stall leben.
Wir sehen im Beispiel, dass die Graphen der beiden linearen Gleichungen y = 9 – x und y = 12 – 2x jeweils Geraden sind.
Ein LGS kann entweder eine, keine oder unendliche viele Lösungen haben. Die Anzahl der Lösungen eines linearen Gleichungssystems kann man an der Lage der entsprechenden Geraden im Koordinatensystem ablesen.
1. Fall: Das LGS hat genau eine Lösung.
I: 2x + 4y = 8
II: 2x – 2y = 2
Wir formen beide Gleichungen nach y um und erhalten
I: y = -0,5x + 1
II: y = x – 1
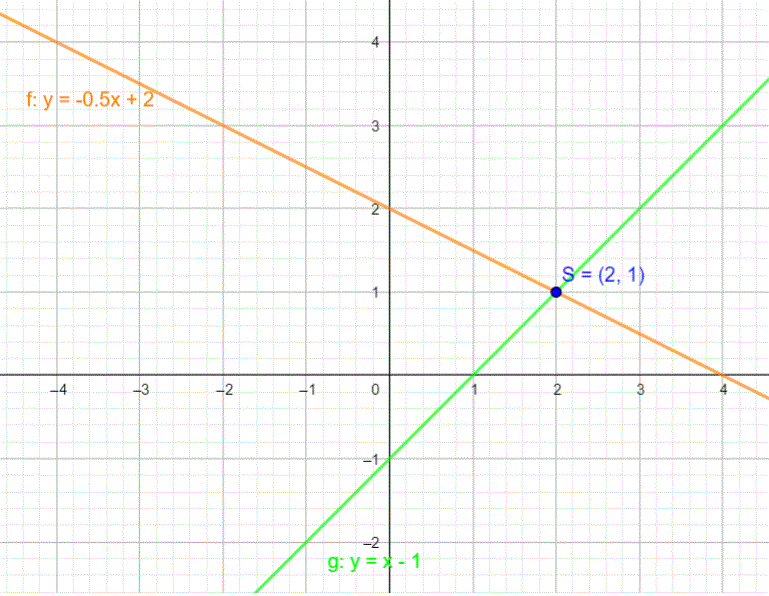
Die Geraden schneiden sich in genau einem Punkt,
S(2 / 1).
Das LGS hat die Lösung x = 2 und y = 1.
Die Lösungsmenge lautet daher \mathbb{L} = {(2 / 1)}
2. Fall: Das LGS hat keine Lösung.
I: -6x + 4y = 2
I:: 6x – 4y = 4
Wir formen beide Gleichungen nach y um und erhalten
I: y = 1,5x + 0,5
II: y = 1,5x – 1
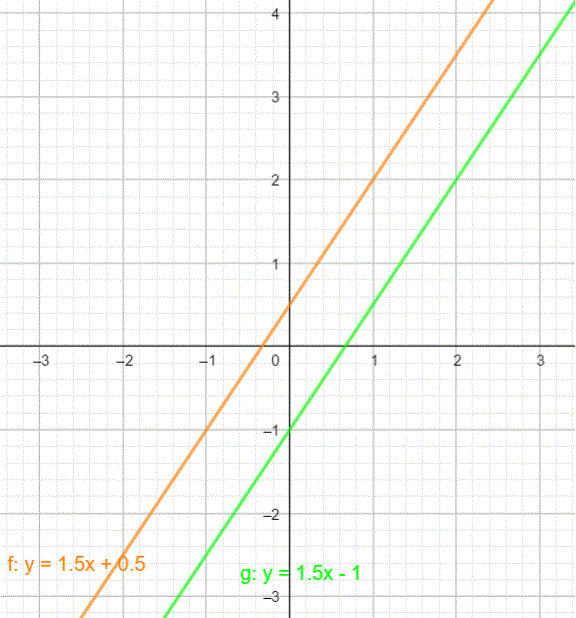
Die Geraden schneiden sich nicht, da sie parallel verlaufen. Das liegt daran, dass sie jeweils die Steigung m = 1,5 haben.
Sie haben daher keinen gemeinsamen Schnittpunkt und somit gibt es für dieses LGS keine Lösung.
Die Lösungsmenge ist leer, \mathbb{L} = { }
3. Fall: Das LGS hat unendlich viele Lösungen.
I: 2x – 2y = -2
II: 4x – 4y = -4
Wir formen beide Gleichungen nach y um und erhalten
I: y = x + 1
II: y = x + 1
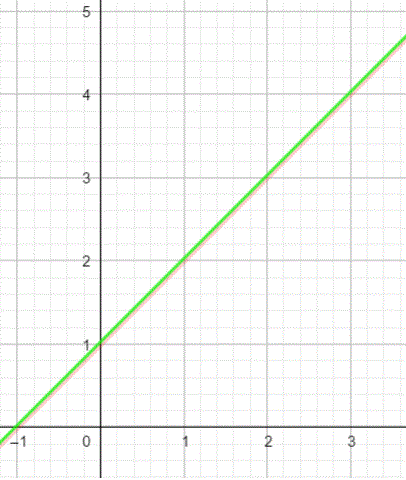
Beide Gleichungen haben die gleiche Steigung m und den gleichen y-Achsenabschnitt b. Daher fallen die Geraden zusammen.
Man kann also alle Punkte der Geraden nehmen, damit beide Gleichungen wahr werden.
Übung
LGS