4. Primzahlen

Eine Primzahl ist eine natürliche Zahl, die nur durch 1 und sich selbst teilbar ist.
Die Primzahlen unter 100 lauten: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 73, 79, 83, 89, 97.
Es gibt unendlich viele Primzahlen.
Primzahlen haben in vielen Bereichen der Mathematik eine Bedeutung.
Jede natürliche Zahl, die größer als 1 und selbst keine Primzahl ist, lässt sich als Produkt von mindestens zwei Primzahlen schreiben.
Beispiel: 6 = 2 • 3; 24 = 2 • 2 • 2 • 2 • 3 = 2^{4} • 3   
Es gibt keine Formel, mit der man Primzahlen berechnen kann.

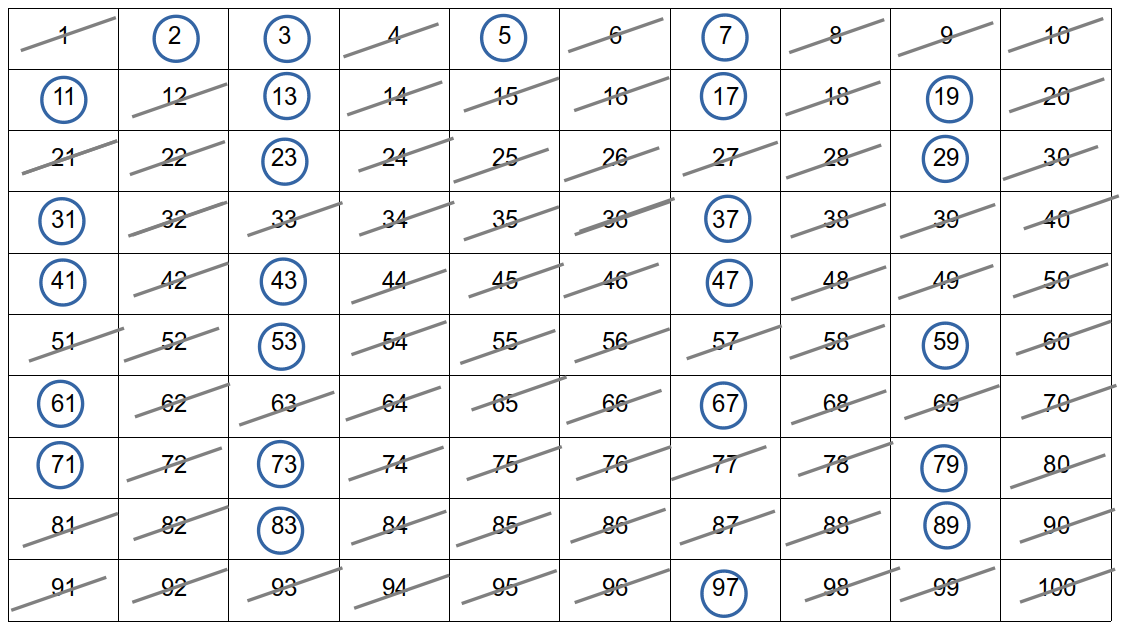
Mithilfe des Sieb des Eratosthenes kann man z. B. prüfen, ob Zahlen Primzahlen sind.
Man notiert alle Zahlen von 1 bis 100 in einer Tabelle.

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49	50
51	52	53	54	55	56	57	58	59	60
61	62	63	64	65	66	67	68	69	70
71	72	73	74	75	76	77	78	79	80
81	82	83	84	85	86	87	88	89	90
91	92	93	94	95	96	97	98	99	100

a) Nun streicht man als erstes die 1 weg, da es sich bei 1 um keine Primzahl handelt.

b) Es folgt die 2. 2 wurde bis jetzt nicht weggestrichen und ist deshalb Primzahl. Wir markieren 2 als Primzahl.

c) Wir streichen nun alle durch 2 teilbaren Zahlen, weil diese nicht Primzahlen sein können.
(Sie hätten jeweils die Teiler 1,2 und sich selbst)

d) Die 3 ist nun die nächste ungestrichene Zahl! Wir markieren 3 als Primzahl.

e) Wir streichen nun alle durch 3 teilbaren Zahlen, weil diese ebenfalls keine Primzahlen mehr sein können.

f) Nun wiederholen wir Schritt d) und e) bis alle Zahlen entweder als Primzahlen markiert, bzw. als Nichtprimzahlen durchgestrichen sind.
Achtung: Diese Schritte müssen nur bis zur Zahl durchgeführt werden, die größer oder gleich der Wurzel des zu überprüfenden Bereich ist. z.B. 10 bei 100, 32 bei 1000, da 10 * 10 = 100 bzw. 32 * 32 = 1024 > 1000

„Quelle: https://lehrerfortbildung-bw.de/u_matnatech/imp/gym/bp2016/fb1/5_m1_mgk/4_loesungen/3_prim/

Sieb des Ertothostenes