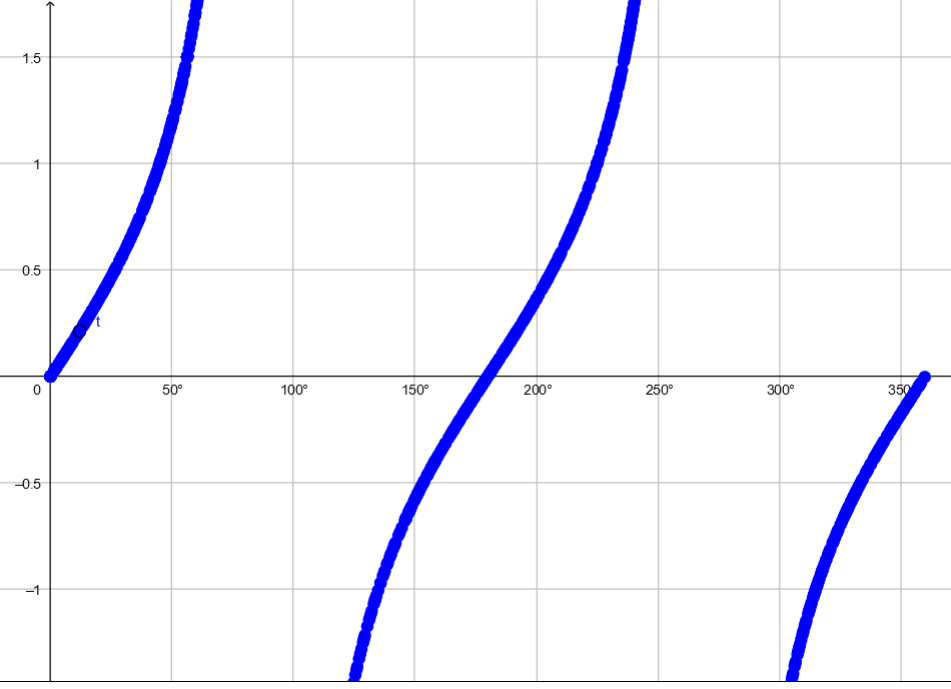
7.1. Trigonometrische Funktionen
Die trigonometrischen Funktionen sind die Sinusfunktion, die Kosinusfunktion und die Tangensfunktion.
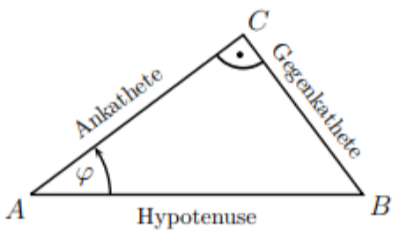
Es ist im rechtwinkligen Dreieck
sin \alpha = \frac{Gegenkathete}{Hyptoneuse}
cos \alpha = \frac{Ankathete}{Hyptoneuse}
tan \alpha = \frac{Gegenkathete}{Ankathete}
Ursprünglich sind die Winkelfunktionen als Seitenverhältnisse in rechtwinkligen Dreiecken und daher nur für Winkel von 0 bis 90 Grad definiert.
Wollen wir nun die trigonometrischen Funktionen auf Winkel anwenden, die größer als 90 Grad sind, dann schauen wir uns hierzu den Einheitskreis an. Dieser hat als Radius eine Längeneinheit (z. B. 1 cm, 1 Zoll, 1 m, … ).
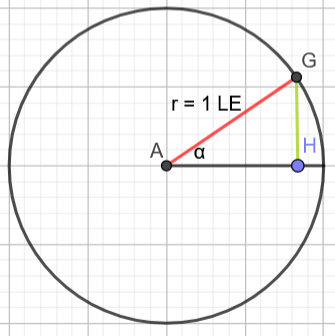
Es ist sin \alpha = \frac{|GH|}{|AG|} = \frac{|GH|}{1} = |GH|
Der Sinuswert des Winkels entspricht somit der Länge der Strecke |GH|.
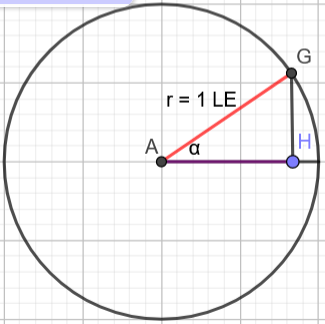
Es ist cos \alpha = \frac{|AH|}{|AG|} = \frac{|AH|}{1} = |AH|
Der Kosinuswert des Winkels entspricht somit der Länge der Strecke |AH|
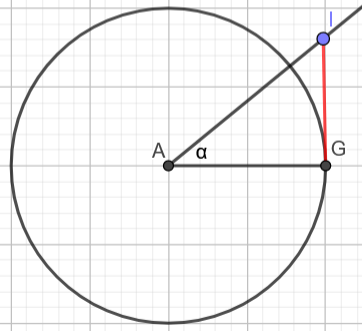
Es ist tan \alpha = \frac{|IG|}{|AG|}
Der Tangenswert des Winkels entspricht somit der Länge der Strecke |IG|.
Je größer der Winkel wird, desto länger ist somit auch |IG|.
Einerseits kann |IG| länger werden als 1 LE, andererseits auch immer größer, je näher sich der Winkel 90 bzw. 270 Grad nähert.
Für genau 90 bzw. 270 Grad gibt es keinen zugehörigen Tangenswert, da in diesem Fall die Strecke |AG| 0 LE lang ist.
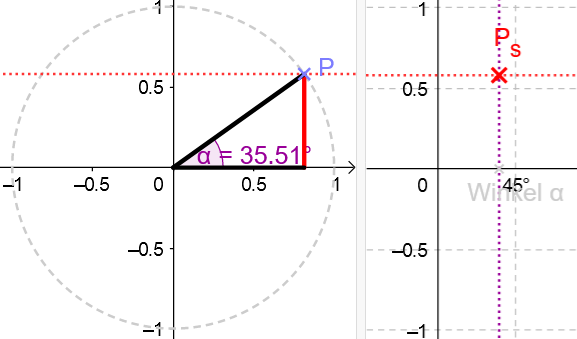
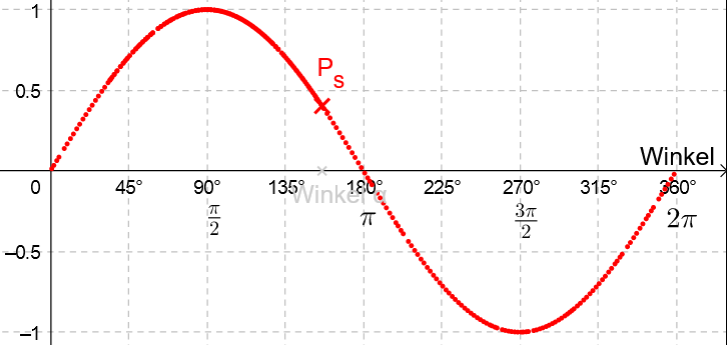
Den Graphen der trigonometrischen Funktionen erhält man, indem man die Länge der Gegenkathete zum Winkel \alpha abträgt. Macht man dies für schrittweise, so ergibt sich die Sinuskurve.
Analog dazu erhält man den Graphen der Kosinusfunktion
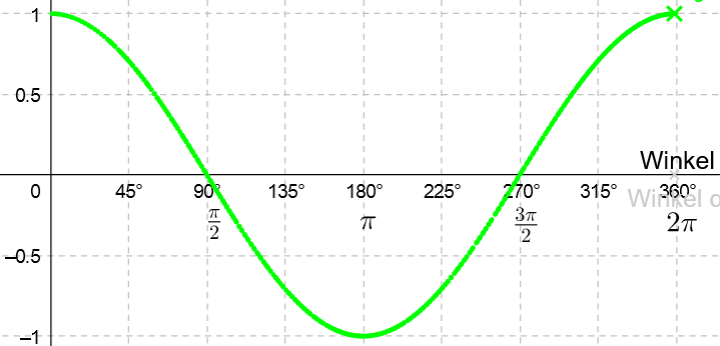
Der Graph der Tangesnfunktion kann nicht in eienem Zug gezeichnet werden, da es, wie oben beschrieben, für 90 und 270 Grad keine Funktionswerte gibt.