1.4. Extrema
Ein Extrempunkt ist entweder der höchste oder der tiefste Punkt auf einem Intervall des Funktionsgraphen. Handelt es sich um den höchsten Punkt, spricht man von einem Maximum oder Hochpunkt. Geht es um den tiefsten Punkt, handelt es sich um ein Minimum oder einen Tiefpunkt.
Je nachdem wie man das Intervall wählt, kann es sich bei einem Extrempunkt um ein lokales Minimum/Maximum (auch relatives Minimum/Maximum genannt), oder um ein globales Minimum/Maximum (auch absolutes Minimum/Maximum genannt) handeln. Um einen Extrempunkt zu finden, bestimmt man zunächst die erste Ableitung der Funktion, also die Tangentensteigung.
Da wo die Tangentensteigung den Wert 0 hat, fällt oder steigt der Graph nicht. Genau dort liegt ein Hoch- bzw. Tiefpunkt.
Aber wo hat die Steigung den Wert 0? Genau da, wo f‘(x) = 0.
Man sucht also die Nullstellen der ersten Ableitung.
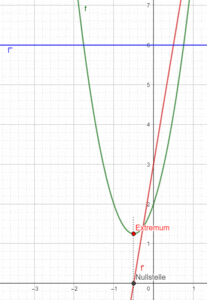
In der Abbildung sieht man, dass da wo der niedrigste Punkt der Parabel ist (Extremum), sich auch die Nullstelle der Ableitungsfunktion (rot) befindet. Ebenso erkennt man, dass links vom Extremum der Graph von f fällt, also hat f‘ negative Werte. Rechts davon steigt der Graph von f, die Werte des Graphen der ersten Ableitung sind dort positiv. Der Graph der zweiten Ableitung ist eine Gerade, die konstant bei y = 6 verläuft und somit positiv ist.
Hat man die Nullstelle der ersten Ableitung bestimmt, so weiss man wo bzgl. der x-Richtung sich das Extremum befindet.
f(x) = 3x² + 3x + 2
f‘(x) = 6x + 3
Setze f‘(x) = 0:
6x + 3 = 0, x = – 0,5
Geht man – 0,5 in x-Richtung liegt, so liegt dort ein Extremum vor.
Dessen Art – Maximum oder Minimum – hat man aber noch nicht bestimmt.
Die Nullstelle der ersten Ableitung setzen wir in die zweite Ableitung ein und überprüfen die Funktionswerte an dieser Stelle. Es gilt nun:
f‘(xE)=0
f‘‘(xE) > 0, dann liegt an der Stelle xE ein Minimum vor.
f‘‘(xE) < 0, dann liegt an der Stelle xE ein Maximum vor.
Gilt f‘‘(xE) = 0, so liegt an der Stelle xE ein Sattelpunkt vor.
Die genaue Koordinate des Extremums bestimmt man, indem man xE in f einsetzt.
Welches entscheiden wir mithilfe der zweiten Ableitung.
f‘‘(x) = 6
f‘‘(–0,5) = 6 > 0. Es liegt somit ein Minimum vor.
Um zu bestimmen wo nun das Extremum im Koordinatensystem liegt, setzt man –0,5 in f ein.
f(–0,5) = 1,25
Somit haben wir bei (–0,5 / 1,25) einen Tiefpunkt vorliegen.
Allgemein gilt zur Bestimmung der Extrema:
Bestimme die Nullstellen der ersten Ableitung: f‘(xE)=0
Setze die gefundenen Nullstellen in die zweite Ableitung ein.
Wenn f‘‘(xE) > 0, dann liegt an der Stelle xE ein Minimum vor. Ist f‘‘(xE) < 0, dann liegt an der Stelle xE ein Maximum vor.
Setze xE in f(x) ein, um die y – Koordinate des Extremums zu bestimmen. E(xE / f(xE))
Übung